Isoperimetric Theorem for Quadrilaterals
Introduction
Among all quadrilaterals with the same perimeter, square has the largest area.
or, equivalently,
Among all quadrilaterals with the same area, square has the smallest perimeter.
The proof is in three steps:
For any quadrilateral (that is not a parallelogram), there is a parallelogram with smaller perimeter but the same area.
For every parallelogram (that is not a rectangle), there is a rectangle with larger area but the same perimeter.
For every rectangle (that is not a square) there is a square of larger area but the same perimeter.
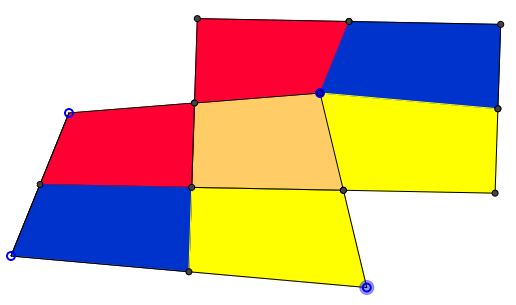
Parallelogram among Quadrilaterals
For any quadrilateral (that is not a parallelogram), there is a parallelogram with smaller perimeter but the same area.
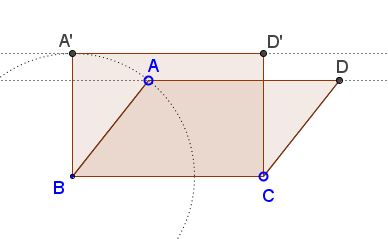
Rectangle among Parallelograms
For every parallelogram, there is a rectangle with larger area but the same perimeter.
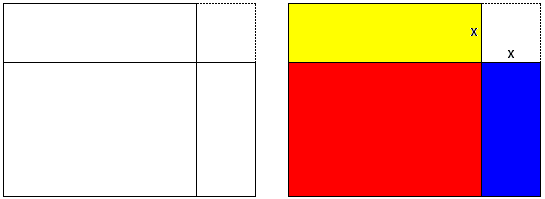
Square among Rectangles
For every rectangle (that is not a square) there is a square of larger area but the same perimeter.
Acknowledgment
The above has been communicated to me in private correspondence by Sidney Kung on 1 March, 2014.
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73582355
