Isoperimetric Theorem for Rectangles

A particular case of the Isoperimetric Theorem says that among all rectangles of a given perimeter, the square has the largest area. (This is of course equivalent to the claim that among all rectangles of a given area the square has the least perimeter.) This particular case of the general theorem is so simple that it was considered suitable for the NJ 4th graders preparing to take the NJ ASK4 test in mathematics. The problem has been posed in the following form:

Mr. Lynch has 80 feet of fencing that he will use to make a garden. His garden can be either a square or rectangular in shape. He wants to choose the shape that will give him a larger planting area.

What shape garden will have a larger area?

If p is the fixed perimeter of the shapes at hand, a - the side of the square - equals p/4: a = p/4. For a rectangle of the same perimeter, the two adjacent sides, say u and v, add up to half of it:

u + v = p/2 = 2a.

If, say u exceeds the side of the square a by some length x, then the other side, v, is shorter than a by the same amount:

u = a + x,
v = a - x.

The area of the rectangle with sides u and v equals uv, or, in our case,

uv = (a + x)(a - x) = a² - x².

Which actually proves the statement of the theorem. Indeed, a² is the area of the square of perimeter p = 4a, whereas a² - x² is the area of a rectangle of the same perimeter for which one of the sides is longer, the other shorter (by the same amount x) than the side of the square. Since x² ≥ 0, a² - x² ≤ a², with equality only when x = 0, i.e. when a rectangle becomes a square.

The problem of Mr. Lynch is solved with p = 80.

The reason I came across this problem is that I live in New Jersey and have a son who is in the 4th grade. Trying to solve the problem, the boy found correctly the area of the square, 400, and checked that the area of the 30×10 rectangle is 300 which is clearly less than the area of the square. He was nowhere near employing the simple algebra as was done above. Sometime beforehand, we practiced mental arithmetic based on the formula for the difference of two squares. (E.g., 38×42 = 1600 - 4 = 1596.) So he was not intimidated by the algebra but still appeared in need of additional explanation.

On first impulse, I tried to explain the algebra. Only later did I realize that the algebra was not needed even as an intermediate step. I believe the boy was absolutely satisfied with the final result.

So, let's draw a square and a rectangle of the same perimeter:

square and rectangle

and put the two together.

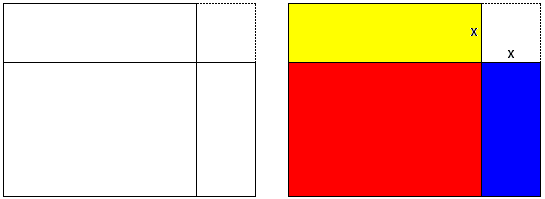
square and rectangle

The area of the square is the sum of the red and yellow areas, that of the rectangle is the sum of the red and blue areas. The red being common to both, it is clear that the area of the square is greater than the area of the rectangle if and only if the yellow area exceeds the blue area. But this is quite simple. The area of a rectangle is the product of the lengths of two adjacent sides. If a is the side of the square, then the yellow area equals x×a whereas the area of the blue region is x×(a - x). And, since, a exceeds a - x for x > 0, we are again done.

This explanation was very acceptable to the boy and at this point we busied ourselves with something else. Later, when I began preparing the diagrams for this page it occurred to me that it is possible to completely avoid using algebra. The boy came to my office to check what I was doing and had observed the diagrams. Wow, he said, this is what we've been talking about. Now, I pointed out, look at the blue and yellow rectangles and the dotted square in the upper right corner. What can you say about their areas. He immediately saw that

yellow = blue + dotted

which clearly implied

yellow ≥ blue.

This was his "Aha!" moment. The problem has been solved.

Reference

  1. ASK 4 Success: Work-A-Text. Mathematics, Instructivision, Inc., 2006

Related material
Read more...

  • Isoperimetric Theorem and Inequality
  • An Isoperimetric theorem
  • Isoperimetric theorem and its variants
  • Isoperimetric Property of Equilateral Triangles
  • Isoperimetric Property of Equilateral Triangles II
  • Maximum Area Property of Equilateral Triangles
  • Isoperimetric Theorem For Quadrilaterals
  • Parallelograms among Quadrilaterals
  • Rectangles among Parallelograms
  • Isoperimetric Theorem For Quadrilaterals II
  • An Isoperimetric Problem in Quadrilateral

    • |Contact| |Front page| |Contents| |Did you know?| |Geometry|

    Copyright © 1996-2018 Alexander Bogomolny

    71534493