Parallelograms among Quadrilaterals

What Might This Be About?

Problem

For every (convex, and, if so, for non-convex) quadrilateral ($ABCD$ below) there is a parallelogram ($OO'B'O''$) below of the same area but smaller perimeter.

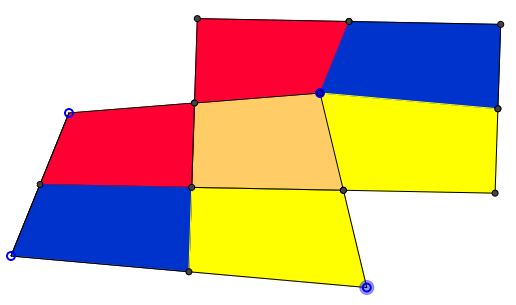
Among all quadrilaterals with the same perimeter parallelogram encloses the largest area

Solution

The proof depends on the following property of bimedians - the lines joining the midpoints of the opposite sides of a quadrilateral.

In a quadrilateral $ABCD,$ $E$ is the midpoint of $AD,$ $G$ the midpoint of $BC.$

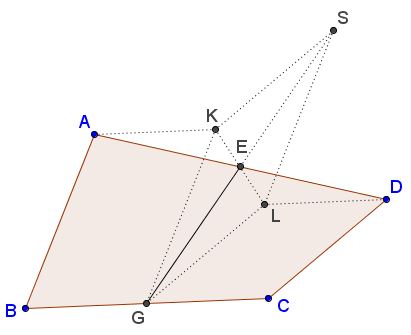
inequality of the length of a bimedian in a quadrilateral

Then $2EG\le GK+KS=GK+GL= AB+CD.$

Apply that to the diagram below:

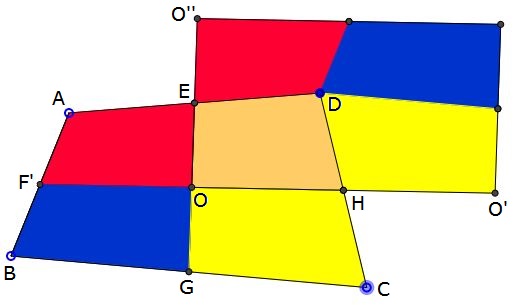
Among all quadrilaterals with the same perimeter parallelogram encloses the largest area

$2OO'=2F'H\le AD+BC.$

And, similarly,

$2OO''=2EG\le AB+CD.$

Note that, by the construction, $OO'B'O''$ is a parallelogram with perimeter

$2(OO'+OO'')\le AD+BC+AB+CD,$

the perimeter of $ABCD.$ The construction (by dissection and rearrangement) makes it obvious that the two quadrilaterals have the same area.

Related material
Read more...

  • Isoperimetric Theorem and Inequality
  • An Isoperimetric theorem
  • Isoperimetric theorem and its variants
  • Isoperimetric Property of Equilateral Triangles
  • Isoperimetric Property of Equilateral Triangles II
  • Maximum Area Property of Equilateral Triangles
  • Isoperimetric Theorem For Quadrilaterals
  • Parallelograms among Quadrilaterals
  • Rectangles among Parallelograms
  • Isoperimetric Theorem for Rectangles
  • Isoperimetric Theorem For Quadrilaterals II
  • An Isoperimetric Problem in Quadrilateral

    • |Contact| |Front page| |Contents| |Geometry|

    Copyright © 1996-2018 Alexander Bogomolny

    71862815