What Is Angle?

Etymologically the angles got to be small [Schwartzman]:

However, the common definition of angle does not refer to the size of the angle at all:

To enable comparison and addition, some texts [Hilbert, Kiselev, O'Daffer] associate with an angle one of two regions into which the two sides of the angle split the plane. One of these is termed the interior and the other the exterior of the angle. In order to compare the angles they should be placed so their interiors intersect while some two sides and the vertices coincide. The angle whose other side is located in the interior of the other angle is declared (and naturally so) the smaller of the two. For addition, we overlap one side of one angle with a side of the other so as to insure that their interiors do not intersect. The two free sides (one from each of the addends) form an angle which is declared the sum of the two.

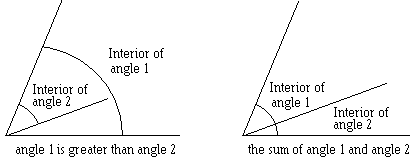
With some caution, we can define straight and right angles. An angle is straight when its sides form a straight line. That angle is right which, when doubled (i.e. added to itself), gives a straight angle. In Euclid's terms (Definition I.10), "When a straight line standing on a straight line makes the adjacent angles equal to one another, each of the equal angles is right." Acute and obtuse angles are smaller and respectively greater than right. Usually, obtuse angles are taken to be smaller than straight, in which case the angles that exceed the straight angle are said to be reflex. A reflex angle so big as to have its two sides overlap is full. (A dynamic illustration is available elsewhere.)

The sum of two acute angles is either acute, right or obtuse. The sum of an obtuse and an acute angle, or of three acute angles, may be reflex. The existence (or admittance) of reflex angles kills all hope that the interior of an angle may be determined from its sides in a natural way.

Handpicking the interior and appending it to the definition almost solves the problem. A difficulty arises only for angles greater than full for which the notion of interior becomes quite dubious. An alternative is to associate angles with angular measure, for example, via the

The authors usually restrict themselves to allowing angles either less than straight [Hilbert, Jacobs] or less than full [Birkhoff]. The angles outside the chosen range are looked at more as algebraic rather than geometric entities. The metamorphosis is commonly implicit. For example, by the time we learn that the sum of the interior angles of a convex n-gon is (n-2)·180°, the latter is perceived as purely an algebraic quantity.

There are two units of angle measurement: degrees and radians. A full angle is equated to 360 degrees which is written as 360° or 2π radians. Radian is in fact a unitless unit. 2π of them is the ratio of the circumference to the radius of a circle and is the same for all circles.

Using angle units the angle classification is summarized as follows: for an angle α,

The Protractor Postulate is mute as to the order of rays in which the difference is taken. Obviously, there are always two possibilities. One produces a positive number, the other a negative one. In elementary geometry, most of the time the order of the rays is ignored so that all angles are positive. But signed angles (also directed, sensed, oriented angles) have their uses. Thus, if an angle is 2-element set {OA, OB} containing two rays with a common vertex, a signed angle is an ordered pair (OA, OB) of two rays. (Tacitly we assume that enumeration of the rays emanating from a point is consistent with a possible orientation of the plane.) One of the rays in a pair (OA) is called initial, the other (OB) terminal, and the difference is calculated from the latter to the former. Thinking of the two as distinict positions of the same ray rotating around a fixed end point, we come with the interpretation of angle as a measure of rotation of a ray around a point. A rotation of a ray is naturally defined by its initial position and the amount of rotation which may include any number of complete revolutions.

In the presence of a selected plane orientation, a pair of a ray and a real number defines a unique rotation. Usually, the counterclockwise rotations are said to be positive; clockwise rotations are negative.

But what is a rotation? Is it possible to define a rotation without first introducing the angle of rotation? Yes, this is possible based on the notion of geometric transformation. Rotation is a geometric transformation with a fixed point that preserves distances. The relationship becomes transparent with the introduction of complex numbers, but it then becomes easy to lose the track of what comes first.

So, usually, elementary geometry texts count on students to have an intuitive idea of angle, introduce angle through the common definition and then often stealthily expand the notion of angle to angles that the definition does not cover. Doing otherwise requires much more serious mathematics than could be safely handled by both students and teachers.

References

1. S. Beckmann, Mathematics for Elementary Teachers and Activities , Addison Wesley, 2004
2. G. D. Birkhoff and R. Beatley, Basic Geometry, AMS Chelsea Publ., 2000, 3^rd edition
3. H. R. Jacobs, Geometry: Seeing, Doing, Understanding, W. H. Freeman and Company, 2003
4. G. A. Jennings, Modern Geometry with Applications, Springer, 1994
5. T. L. Heath, Euclid: The Thirteen Books of The Elements, v. 1, Dover, 1956
6. D. Henderson, Experiencing Geometry, Prentice Hall, 2004
7. D. Hilbert, Foundations of Geometry, Open Court, 1999
8. Kiselev's Geometry. Book I. PLANIMETRY, adapted from Russian by Alexander Givental, Sumizdat, 2006.
9. P. O'Daffer, Mathematics For Elementary School Teachers, Addison-Wesley, 2002
10. D. Pedoe, Geometry: A Comprehensive Course, Dover, 1988
11. S. Schwartzman, The Words of Mathematics, MAA, 1994

|Contact| |Front page| |Contents| |Geometry| |Up| |Store|

Copyright © 1996-2012 Alexander Bogomolny