Circle, Its Perimeter and Area
Circle is the set of points on a fixed distance from a given point; the latter is called the center while that distance is the radius of the circle. The word radius has also another meaning: a line segment from the center to any point on the circle is also called radius. A line joining any two points on a circle is called chord; a chord that passes through the center is known as a diameter diameter is formed by two radii.
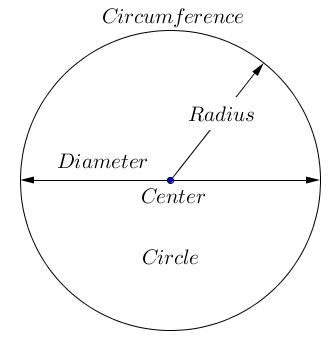
Sometimes - if not often - the terminology differs: Circle is the plane region enclosed by a curve that is called circumference and is the circle in the sense of the opening paragraph above. To compound, regardless of the usage, circumference stands for two things: the curve and the length of that curve, or perimeter of the circle, exactly like the notions of radius and diameter which could be line segments and also their respective lengths.
Commonly, the radius is denoted $R$ or $r$, diameter $D$ or $d,$ e.g., $D=2R;$ the circle may be denoted as $(O),$ $O(R),$ $C(O,R)$ depending on conventions and experiences.
All circles are similar. This fact implies that the circumference and area of a circle are functions of its radius: linear function, for the circumference; quadratic function, for the area. Both are homogeneous, with related coefficients: circumference $C=2\pi R,$ area $S=\pi R^2.$ Why the two are related? There are at least two explanations: one by Leonardo da Vinci, another by Rabbi Abraham bar Hiyya Hanasi. According to da Vinci, the area of a circle $O(R)$ is the same as that of a rectangle with base $\pi R$ and side $R,$ i.e., $\pi R\cdot R=\pi R^2.$ According to Rabbi Abraham bar Hiyya, the area of a circle equals that of a triangle with base $2\pi R$ and altitude $R:$ $\displaystyle\frac{1}{2}2\pi R\cdot R=\pi R^2.$ Both explanations rely on the concept of the limit. Unlike the areas of polygonal shapes that could be reduced by a decomposition to a union of a finite number of triangles, shapes with curved boundaries - like circle - require calculus to define their boundary length and area.
To see how it works for area, place a circle on a square grid and then refine the grid by dividing squares into four small ones. Imagine that a process goes on.
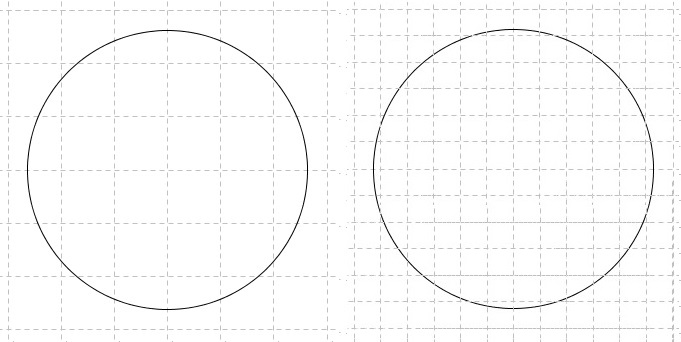
In every case, trace the grid lines closest to the circle - one from inside, the other outside - without crossing it.
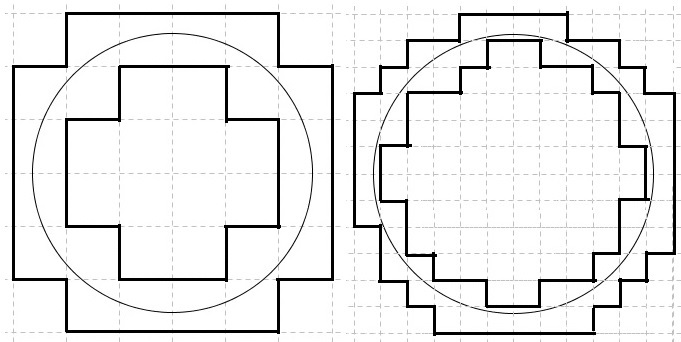
This, for every grid, creates two polygons whose are it is easy to calculate. But more importantly, as we keep grids refined, the areas between the two polygons become closer and closer. This can be illustrated with just two grids. Let the side length of the square on the left is $1;$ on the right it will be $\displaystyle\frac{1}{2}.$ There are $20$ squares between polygons on the left, making the difference in areas $20\cdot 1=20.$ On the right there are $50$ squares of side $\displaystyle\frac{1}{2}$ so that the area between them is $\displaystyle 50\cdot\bigg(\frac{1}{2}\bigg)^2=\displaystyle\frac{50}{4}=12.5.$
It can be shown rigorously that the difference in the "inner" and "outer" polygonal areas shrinks to zero, telling us that both sequences of polygonal areas have the same limit. This limit is found to be exactly $\pi R^2$ - a formula to remember.
To define the circumference, one needs a different kind of approximation. The classical way of doing that is due to Archimedes: the circle is approximated from inside and outside by regular polygons.
References
- J. Hadamard, Leçons de géométrie élémentaire, tome I, 13e édition, 1947, Editions Jacques Gabay, 1988, ISBN 2-87647-038-1.
- D. Hilbert, Foundations of Geometry, Open Court, 1999
- Kiselev's Geometry. Book I. PLANIMETRY, adapted from Russian by Alexander Givental, Sumizdat, 2006.
- What Is Area
- Elementary Introduction into the Concept of Area
- Area of Rectangle
- Area of Parallelogram
- Area of Triangle
- Area and Perimeter of Circle
- Equidecomposition of a Triangle and a Rectangle: first variant
- Pick's Theorem
- Area of a Circle by Rabbi Abraham bar Hiyya Hanasi
- Area of a Circle by Leonardo da Vinci
- Volume and Area of Torricelli's Trumpet
|Contact| |Front page| |Contents| |Algebra| |Up|
Copyright © 1996-2018 Alexander Bogomolny
73561963
