Squares on Sides of a Quadrilateral: What is this about?
A Mathematical Droodle

Discussion

Discussion

Erect similarly oriented squares on the sides of a quadrilateral ABCD. Denote their centers successively O₁, O₂, O₃, and O₄. Then

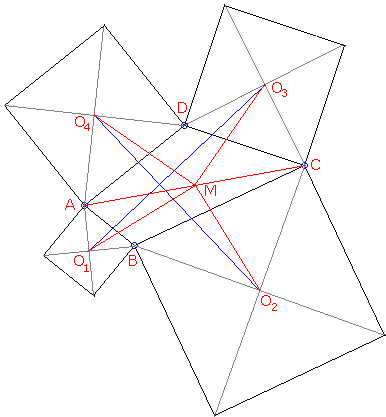
(1)	O1O3 = O2O4 and
(2)	O1O3 O2O4.

Proof

Let M be the midpoint of AC. By the Finsler-Hadwiger theorem,

	MO1 = MO2 and
	MO1 MO2

and also

	MO3 = MO4 and
	MO3 MO4.

Therefore, triangles MO₁O₃ and MO₂O₄ are equal and one is a rotation of the other through 90^o. Hence, (1) and (2) hold.

Remark

1. If any two adjacent vertices of a quadrilateral coalesce into a point, the statement just proven becomes a property of the Bride's Chair configuration.

2. The theorem we just proved is attributed to Van Aubel (Von Aubel in [Gardner, p. 176-178]) could also be found in [de Villiers, Yaglom, Finney] among others.

3. The argument falls through in case one of O₁O₃ or O₂O₄ is of zero length. This case is considered elsewhere. There it is shown that the two distances are either both 0 or not. The former case occurs iff the diagonals of the quadrilateral are equal and perpendicular.

References

1. E. J. Barbeau, M. S. Klamkin, W. O. J. Moser, Five Hundred Mathematical Challenges, MAA, 1995, #320b
2. M. de Villiers, The Role of Proof in Investigative, Computer-based Geometry: Some Personal Reflections, in Geometry Turned On, MAA Notes 41, 1997, pp. 15-24
3. R. L. Finney, Dynamic Proofs of Euclidean Theorems, Math Magazine, 43, pp. 177-185.
4. M. Gardner, Mathematical Circus, Vintage, 1981
5. I. M. Yaglom, Geometric Transformations I, MAA, 1962