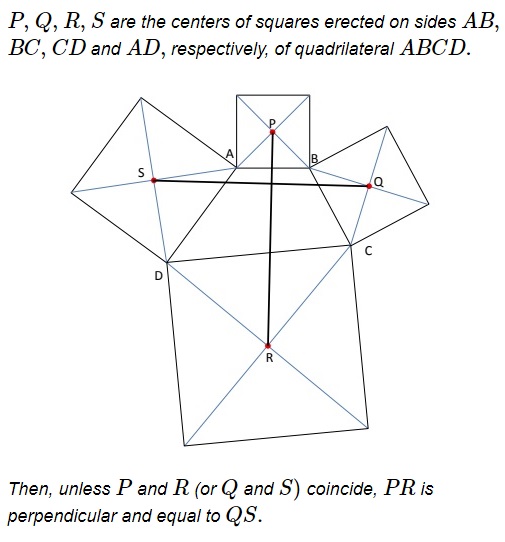
Van Aubel's Theorem for Quadrilaterals And Generalization
Theorem
G. R. Jayanth
28 December 2017
Proof
Reflect the point $P$ about the line $AB.$ Let the reflection be $P'.$ Likewise, let $Q'$ be the reflection of $Q$ about the line $BC.$ To establish Van Aubel's theorem, we show that the triangles $P'QS$ and $Q'PR$ are congruent and rotated with respect to each other by $90^{/circ}.$
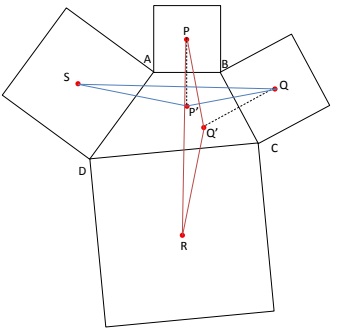
We start the proof by first considering triangle $P'QS$ where we try to determine the length of sides $P'Q$ and $P'S,$ along with the included $\angle QP'S.$ To do the former, we focus on triangle $P'BQ.$
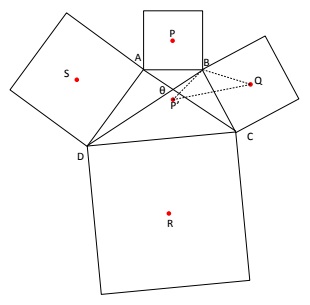
Since $P'$ is the reflection of $P$ about $AB,$ we note that $APBP'$ is a square.
Thus, $\displaystyle P'B=\frac{AB}{\sqrt{2}}.$
Similarly, $\displaystyle BQ=\frac{BC}{\sqrt{2}}.$
Further, since $\angle ABP'=\angle CBQ= 45^{\circ},$ it can be seen that $\angle ABC=\angle P'BQ.$
From ##1-3, triangles $ABC$ and $P'BQ$ are similar.
Thus, $\displaystyle P'Q=\frac{AC}{\sqrt{2}}$ and the line $P'Q$ is tilted with respect to $AC$ by $45^{\circ}.$
Repeating the same arguments for the triangles $DAB$ and $SAP',$ we see that these two triangles are also similar.
Thus, $\displaystyle P'S=\frac{BD}{\sqrt{2}}$ and the line $SP$ is tilted with respect to $DB$ by $-45^{\circ}.$
If $\theta$ represents the angle between the diagonals $AC$ and $BD,$ it can be noted from ##4-5 that $\angle SP'Q= 90^{\circ}+\theta.$
Next we consider triangle Q'PR. By following very similar steps as that done above we can conclude the following:
Triangles $Q'CR$ is similar to triangle $BCD.$ Thus, $\displaystyle Q'R=\frac{BD}{\sqrt{2}}$ and the line $Q'R$ is tilted with respect to $DB$ by $+45^{\circ}.$
Triangles $Q'BP$ is similar to triangle $CBA.$ Thus, $\displaystyle Q'P=\frac{AC}{\sqrt{2}}$ and the line $Q'P$ is tilted with respect to $AC$ by $-45^{\circ}.$
Likewise, it can be noted from #7-8 that $\angle PQ'R= 90^{\circ}+\theta.$
From #4-9, we conclude $\displaystyle P'Q=Q'P=\frac{AC}{\sqrt{2}},$ $\displaystyle P'S=Q'R=\frac{BD}{\sqrt{2}}$ and $\angle SP'Q=\angle PQ'R=90^{\circ}+\theta.$
The latter implies that triangles $P'QS$ and $Q'PR$ are congruent. Therefore $PR=QS.$ Further, #4 and #8 imply that $P'Q$ and $Q'P$ are at $90^{\circ}$ to each other, while #5 and #7 imply that $P'S$ and $Q'R$ are at $90^{\circ}$ to each other. This implies that $PR$ and $QS$ are also at $90^{\circ}$ to each other.
This proves Van Aubel's Theorem.
Generalization
Let $ABCD$ be any quadrilateral. Erect a right triangle $APB$ on $AB$ such that it is right-angled at $P.$ Erect similarly right triangles $BQC,$ $CRD$ and $DSA$ on $BC,$ $CD$ and $DA,$ respectively, such that, at any vertex of the quadrilateral, the two triangles that share this vertex possess the same angle (e.g., at vertex $A,$ $\angle PAB=\angle SAD$ and at vertex $B,$ $\angle PBA=\angle QBC,$ etc.)
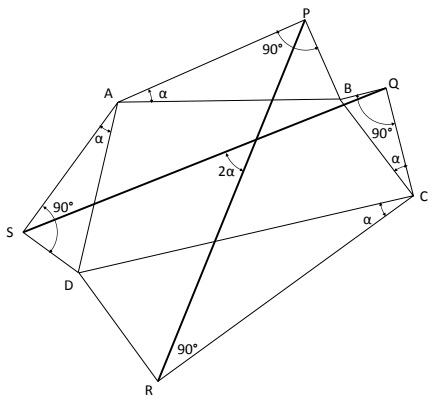
Then, $PR=QS$ and the angle between $PR$ and $QS$ is twice $\angle PAB.$
Note: For the special case of $\angle PAB 45^{\circ},$ $PR$ and $QS$ would be perpendicular to each other, and the configuration reduces to Van Aubel's theorem.
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73570729
