Extra Feature of Van Aubel Configuration
What Might This Be About?
Problem
Given quadrilateral $ABCD,$ let $E,F,G,H$ be the centers of the similarly oriented squares constructed on its sides. Define points $X,V$ as the midpoints of $AC$ and $BD$ and $U,W$ as the midpoints of $EG$ and $FH.$
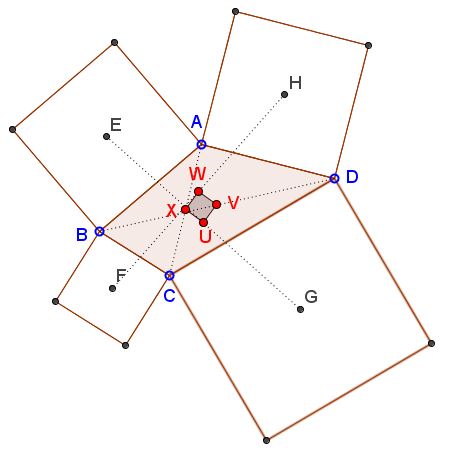
Then $UVWX$ is a square.
Note that this statement nicely complements van Aubel's theorem.
Proof 1

We'll use complex numbers. Treating points as complex numbers,
$\begin{align}\displaystyle E&=\frac{A+B}{2}+i\frac{A-B}{2},\\ F&=\frac{B+C}{2}+i\frac{B-C}{2},\\ G&=\frac{C+D}{2}+i\frac{C-D}{2},\\ H&=\frac{D+A}{2}+i\frac{D-A}{2}.\\ \end{align}$
so that
$\displaystyle \begin{align} U &= \frac{E+G}{2}=O+i\frac{A-B+C-D}{4},\\ W &= \frac{F+H}{2}=O-i\frac{A-B+C-D}{4}. \end{align}$
where $\displaystyle O=\frac{A+B+C+D}{4}.$ Obviously, $O$ is the midpoint of $UW.$ Also, by the definition, if $\displaystyle X=\frac{A+C}{2}$ and $\displaystyle V=\frac{B+D}{2}$ then $O$ is also the midpoint of $VX.$ This already shows that $UVWX$ is a parallelogram. We shall now show that its diagonals are orthogonal. Indeed,
$\displaystyle \begin{align} U-O &= i\frac{A-B+C-D}{4},\\ X-O &= \frac{A-B+C-D}{4}, \end{align}$
exactly meaning that $OU\perp OX.$
Proof 2
Rotate triangle $AXE$ around $E$ by $90^{\circ}$ clockwise. Then $A$ goes to $B$ and $X$ to point $X'$ such that $\angle EBX'=\angle EAX.$ Similarly, if we rotate $\Delta CXF$ around $F$ we get point such that $\angle FBX''=\angle FCX.$
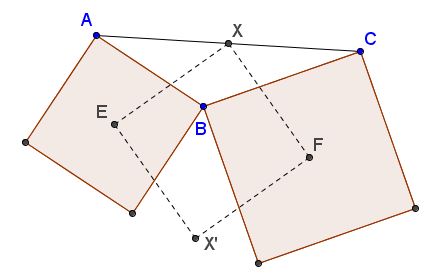
But, by sum of angles in pentagon $AEBFC,$ we get that
$\angle EAX+\angle FCX+\angle EBF=360^{\circ},$
implying that $X''=X'.$ So we get that $FX=FX',$ $EX=EX',$ which says that $EXFX'$ is a kite (deltoid), and $\angle XEX'=\angle XFX'=90^{\circ},$ so it's a square. (This is also the content of the Finsler-Hadwiger theorem.)
Thus, the counterclockwise rotation around $X$ by $90^{\circ}$ moves $E$ to $F.$ Similarly, same rotation moves $G$ to $H.$ So segment $EG$ moves onto $FH,$ and $U$ to $W.$ It follows that $XU=XW$ and $\angle UXW=90^{\circ}.$ Similarly, $VW=VU$ and $\angle WVU=90^{\circ},$ so $UVWX$ is another kite with two right angles and, hence, a square.
Proof 3
The Petr-Douglas--Neumann theorem (of which van Aubel's theorem is a consequence) can be best understood and proved from a spectral point of view (see references below).
Any quadrilateral $q=(a,b,c,d)$ of the complex plane can be expressed by its discrete Fourier series $q=\displaystyle\sum_{k=0}^3 \gamma_kf_k$. The regular quadrilaterals $f_0=(1,1,1,1)$, $f_1=(1,i,-1,-i)$, $f_2=(1,-1,1,-1)$, $f_3=(1,-i,-1,i)=\overline{f_1}$ form the Fourier base of $\mathbb{C}^4$ and the Fourier coefficients $\gamma_k$ are the dot products $\gamma_k=q\cdot\overline{f_k}/4$. Parallelograms correspond to $\gamma_2=0$.
Let $T(q)$ be the quadrilateral obtained by erecting isosceles right-angled right-hand ears on the sides of $q$. The transformation $T$ is linear, i.e., $T(q)=\sum \gamma_kT(f_k)$, and the Fourier base vectors are eigenvectors of $T$: $T(f_0)=f_0$, $T(f_1)=(1+i)f_1$, $T(f_2)=if_2$, $T(f_3)=(0,0,0,0)$. The transformation $T$ deletes the $f_3$ spectral line of $q$.
Let $q''=(c,d,a,b)$ be the quadrilateral $q$ after a shift of its vertices by two: $q''=\sum(-1)^k\gamma_kf_k$. The midpoints of the diagonals of $q$ and of $T(q)$ form the quadrilaterals $(q+q'')/2=\gamma_0f_0+\gamma_2f_2$ and $T(q+q'')/2=\gamma_0f_0+i\gamma_2f_2$, respectively. These are perpendicular and congruent (quadruply covered) segments with midpoint $\gamma_0$, the centroid of $q$ and $T(q)$.
References
G. Nicollier, Convolution Filters for Polygons and the Petr--Douglas--Neumann Theorem, Beitr. Algebra Geom. 54 701--708 (2013).
G. Nicollier, Convolution Filters for Triangles, Forum Geom. 13 61--85 (2013)
Acknowledgment
The statement has been posted by Dao Thanh Oai (Vietnam) at the CutTheKnotMath facebook page to which in the comments Wojtek Wawrów added Proof 2. Proof 3 was communicated to me by Gregoire Nicollier via email.
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73581932
