Twin Segments in Four Semicircles
What Might This Be About?
Problem
The problem has been posted by Miguel Ochoa Sanchez (Peru) at the CutTheKnotMath facebook page as a colorful photo
$M,N,P,Q$ are the midpoints of the four arcs, as shown below:
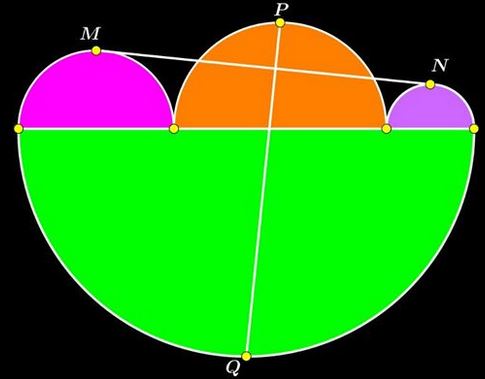
Prove that $MN=PQ$ and $MN\perp PQ.$
Proof
Let the arcs be $(AB),(BC),(CD),(AD)$ with the centers $E,F,G,H$ and radii $a,c,b,a+b+c,$ respectively.
Draw a line through $F$ parallel to $MN$ and let it intersect $EM$ in $J$ so that $FJ\parallel MN.$ Let $I$ on the tangent to $(AD)$ at $Q$ satisfy $GI\perp AD.$
There could be a few of different configurations of which we shall consider just one $(b\gt a, c\gt (a+b)/2).)$:
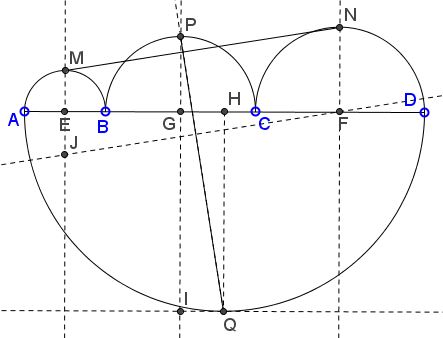
The right triangles $EFJ$ and $IPQ$ are equal. Indeed, $EJ=b-a=IQ$ and $EF=a+b+2c=IP.$ It follows that $MN=FJ=PQ.$ The two are also perpendicular as the hypotenuses of two equal right triangles in which the corresponding legs are perpendicular.
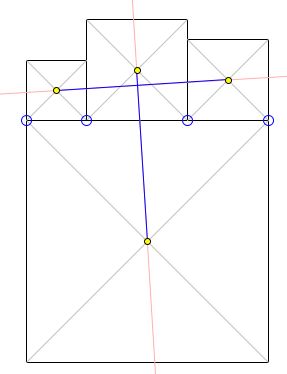
Matt Enlow has observed on twitter that the above is a special case of van Aubel's theorem for quadrilaterals.
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73579750
