Right Isosceles Triangles on Sides of a Quadrilateral
What is this about?
A Mathematical Droodle

Explanation

|Activities| |Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny

The applet may suggest several related properties of a quadrilateral formed by the centers of the squares constructed on the sides of a quadrilateral.

Let P, Q, R, S be the centers of the squares constructed on the sides of a quadrilateral. Then

  1. The quadrilateral PQRS is orthodiagonal and the diagonals are equal in length.

    right isosceles triangles on sides of a quadrlateral, case 1

  2. If the squares are drawn on the sides of quadrilateral with successive apexes P, Q, R, S - internal to the quadrilateral and neither P and R nor Q and S coincide, then PR is orthogonal to QS.

    right isosceles triangles on sides of a quadrlateral, case 1

  3. If the squares are drawn on the sides of quadrilateral with successive apexes P, Q, R, S - internal to the quadrilateral, then P and R coincide iff Q and S coincide.

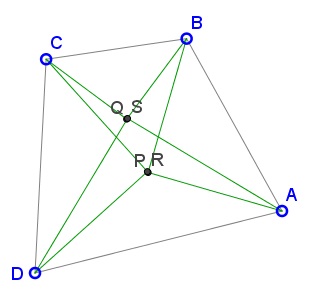
    right isosceles triangles on sides of a quadrlateral, case 3

  4. If the squares are drawn on the sides of quadrilateral with successive apexes P, Q, R, S, so that P and R are internal whilst Q and S are external to the quadrilateral, then if P, Q, S are collinear then so are R, Q, S. In particular, if P and R coincide then P, Q, R, S are collinear.

    right isosceles triangles on sides of a quadrlateral, case 4

Complex numbers come in handy to help solve this problem. Let a, b, c, d be the complex numbers corresponding to the vertices A, B, C, and D and, similarly, p, q, r, s for the points P, Q, R, S. In general, we underscore this relationship as A(a), B(b), etc.

For two points U(u) and V(v), define W(w) via

(1) w = (1 - μ)u + μv,

where μ = (1 + i)/2, is the apex of the right isosceles triangle with base UV such that UVW is oriented counterclockwise. Thus, assuming ABCD presents the positive orientation, we express points (or rather the corresponding complex numbers) P, Q, R, S in terms of the vertices as follows

(2) p = (1 - μ)a + μb,
q = (1 - μ)b + μc,
r = (1 - μ)c + μd,
s = (1 - μ)d + μa.

The diagonals ac and bd are found to be (I use the underline to distinguish say the number uv = v - u corresponding to the segment joining points U and V from the product uv = u·v)

(3) ac = c - a and
bd = d - b.

The two are orthogonal iff

(4) i·ac = bd.

Similarly, the segments PR and QS joining the apexes of our isosceles triangles are represented by

pr = (1 - μ)(c - a) + μ(d - b) and
qs = (1 - μ)(d - b) + μ(a - c),

or,
(5) pr = (1 - μ)ac + μbd and
qs = (1 - μ)bd - μac.

The two are orthogonal iff i·pr = qs. In view of (4), we see that

(6)
i·pr= i(1 - μ)ac + iμbd
 = (1 - μ)bd - μac
 = qs.

So (4) implies (6). Conversely, assume i·pr = qs. Then from (5)

(7) i(1 - μ)ac + iμbd = (1 - μ)bd - μac.

Using

i·μ = -(1 - μ) and
i·(1 - μ) = μ

we reduce (7) to

μac - i(1 - μ)bd = (1 - μ)bd - μac,

or,

(8) μ/(1 - μ)·ac = bd.

But μ/(1 - μ) = (1 + i)/(1 - i) = (1 + i)2/2 = 2i/2 = i. So (8) implies i·ac = bd. This is of course assuming neither pr = 0 or qs = 0. Now, what if pr = 0 say? Then (6) implies that also qs = 0. Obviously, (6) also yields the reversed implication.

Finally, assume Q(q) and S(s) are defined so that BCQ and DAS have negative orientation causing Q and S outside ABCD. In this case (2) is replaced by

(2') p = (1 - μ)a + μb,
q = μb + (1 - μ)c,
r = (1 - μ)c + μd,
s = μd + (1 - μ)a.

P = R is still equivalent to (4). We observe from (2') that (p + r)/2 = (q + s)/2, and, since p = (p + r)/2 = r iff P = R, it follows that if P = R then it serves as the midpoint of QS.

(It also appears that in the latter case, the point of intersection of the diagonals also lies on QS. How come?)

Remark

When all four triangles have the same orientation it was shown elsewhere that PR and SQ are equal and perpendicular. However, the argument falls through when either has zero length.

(There is an additional exploration of this configuration.)

Related material
Read more...

  • Right Triangles on Sides of a Square
  • Equilateral Triangles On Sides of a Parallelogram
  • Equilateral Triangles On Sides of a Parallelogram II
  • Equilateral Triangles on Sides of a Quadrilateral
  • Similar Triangles on Sides of a Quadrilateral
  • Squares on Sides of a Quadrilateral
  • Extra Feature of Van Aubel Configuration
  • Further properties of Van Aubel Configuration
  • Van Aubel's Theorem for Quadrilaterals and Generalization

    • |Activities| |Contact| |Front page| |Contents| |Geometry|

    Copyright © 1996-2018 Alexander Bogomolny

    72203585