Further properties of Van Aubel Configuration
What Might This Be About?
Problem
Let $ABC$ be a triangle, $M_a$ the midpoint of $BC,$ $H$ the orthocenter of $\Delta ABC,$ $V_b,V_c,V'_b,V'_c$ the centers of the four squares, as in the diagram below:
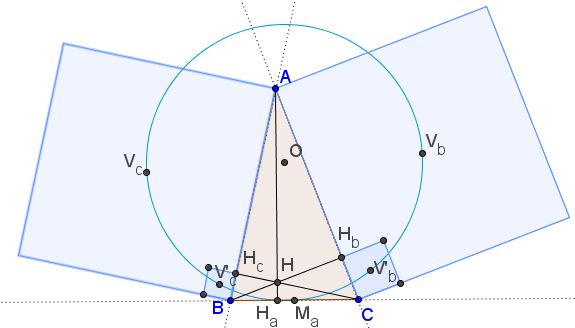
Show that:
Six points $V_b,V'_b,M_a,H_a,V_c,V'_c$ lie on a circle.
$V_bV_c$ is a diameter of this circle.
Reflection $A'$ of $A$ in center of this circle is a fixed point, independent of $A.$
Note that this statement nicely complements van Aubel's theorem.
Proof
Let the two squares on the sides of $\Delta ABC$ be $ABGF$ and ACDE.$ Let $I$ be the midpoint of $EF.$ By the Finsler-Hadwiger theorem $M_{a}V_{b}IV_{c}$ is a square, making the fur points $M_{a},V_{b},I,V_{c}$ concyclic, with $V_{b}V_{c}$ a diameter of their circumcircle. Let it be $(O).$
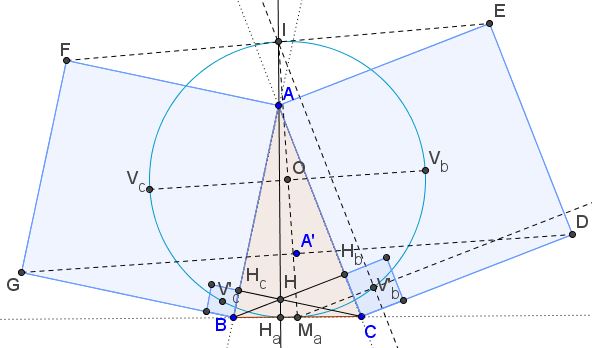
Triangles $AEF$ and $ABC$ are friendly so that the extension of the median $AI$ in $\Delta AEF$ is an altitude in $\Delta ABC.$ In other words, $A$ lies on $IH_a.$ From $IM_a$ being a diameter of $(O)$ and $IH_{a}\perp H_{a}M_{a}$ it follows that $H_a\in(O).$
Redefine $V'_b$ to lie on the intersection of the line through $I$ parallel to $AC$ and the line through $M_a$ parallel to $BH_b.$ First of all, this causes $\angle IV'_{b}M_a =90^{\circ}$ and, therefore, $V'_b\in (O).$ It remains to be shown that $V'_b$ is the center of the square with side $CH_b.$ Now, $M_a$ is the midpoint of side $BC$ in $\Delta BCH_b$ so that $V'_b$ is equidistant from $C$ and $H_b.$ Moreover, $\angle V_{c}V'_{b}I=\angle V_{c}M_{a}I=45^{\circ},$ due to the Finsler-Hadwiger theorem. Thus $V'_{b}$ is indeed the center of the square with side $CH_b.$ Similarly we show that $V_c$ also lies on $(O).$
$V_{b}V_c$ is the midline in $\Delta ADG$ parallel to $DG.$ It follows that $AO$ meets $DG$ at a point at the same distance to $O$ as $A,$ i.e. $A'.$ In addition, $O$ being the midpoint of $V_{b}V_c,$ $A'$ is the midpoint of $DG.$ By Bottema's theorem, $A'$ does not depend on $A.$
Acknowledgment
The statement has been posted by Dao Thanh Oai (Vietnam) at the CutTheKnotMath facebook page. There are three addional solutions posted at the artofproblemsolving.org site.
Extra
Points $V_c,A',H_b,V'_b$ are collinear.
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73580911
