Square out of a QuadrilateralHere is problem 11328 (proposed by Dmitris Vartziotis) from the American Mathematical Monthly, 114 (December 2007): Let ABCD be a convex quadrilateral. Let P be the point outside ABCD such that angle APB is a right angle and P is equidistant from A and B. Let points Q, R, and S be given by the same conditions with respect to the other three edges of ABCD. Let J, K, L, and M be the midpoints of PQ, QR, RS, and SP, respectively. Prove that JKLM is a square. Putting it a little differently, let ABP, BCQ, CDR, and DAS be right isosceles triangles, with right angles at P, Q, R, S. Let J, K, L, and M be the midpoints of PQ, QR, RS, and SP, respectively. Prove that JKLM is a square.
 |Activities| |Contact| |Front page| |Contents| |Geometry| |Store| Copyright © 1996-2012 Alexander Bogomolny Square out of a QuadrilateralLet ABP, BCQ, CDR, and DAS be right isosceles triangles, with right angles at P, Q, R, S. Let J, K, L, and M be the midpoints of PQ, QR, RS, and SP, respectively. Prove that JKLM is a square. In the applet below, check the "Hint" box.
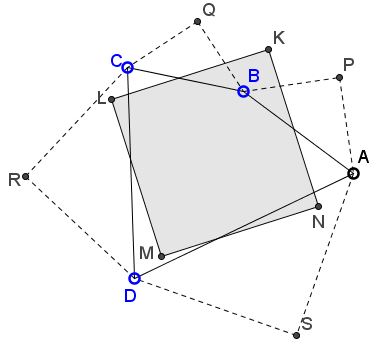
By van Obel's theorem, the diagonals PQ and RS are equal and perpendicular. Lines KL, LM, MN, NK are the midlines,midlines,altitudes,medians,angle bisectors of triangles QRS, RSP, SPQ, PQR so that NoteA theorem by Jesse Douglas shows that the order of the two operations: 1) forming right isosceles triangles and 2) taking the midpoints, is not important. A square pops up regardless of the order in which the operations are performed. |Activities| |Contact| |Front page| |Contents| |Geometry| |Store| Copyright © 1996-2012 Alexander Bogomolny |
| 40620893 |
