Similarity Is About Proportion - And Ways to Look at It
In his commentary on Euclid I.47 (the famous proof of the Pythagorean Theorem), Sir Thomas L. Heath, following Proclus, squarely attributes the proof to Euclid and then speculates that, if Pythagoras did possess a proof of the eponymous theorem, that would in all likelihood have been based on similarity of triangles, i.e. on the theory proportion. Heath observes that, The possible proofs by means of proportion would seem to be practically limited to two.
One is a variant of Proof #6 on the Pythagorean page, the other along the lines of Euclid VI.31.
Making use of algebraic notations, the former may be represented by the following diagram:
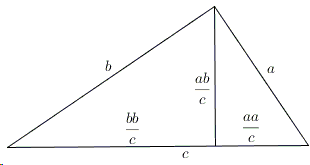
Here a right triangle with legs \(a\) and \(b\) and hypotenuse \(c\) is split into two by the altitude from the right angle. All three triangles are similar but the small ones have \(a\) and \(b\) as the hypotenuses. Their collinear sides that measure \(\displaystyle\frac{aa}{c}\) and \(\displaystyle\frac{bb}{c}\) add up to the hypotenuse \(c\) of the large triangle, implying \(\displaystyle\frac{aa}{c}+\frac{bb}{c}=c\), and the Pythagorean theorem follows.
Heath proposes that this, unlike Euclid VI.31, was most likely within the abilities and knowledge of Pythagoras.
Interestingly, under the common caption of (algebraic) Proof 1, Elisha Loomis lists no less than nine possible ways of exploiting similarity of the three triangles, and then another one as Proof 54. None of these, in my view, is as transparent as that implied by the diagram below:
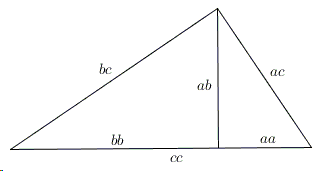
This is a natural simplification of the "unfolded" version:
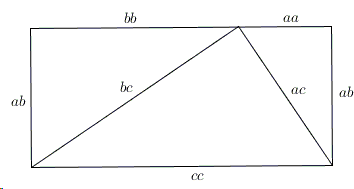
It appears that using products (or homotheties, if you will) instead of ratios, sheds extra light on the derivation. May Pythagoras have the same insight?
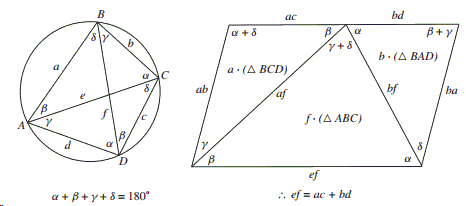
The same approach leads to pretty proofs - proofs without words - of several other theorems. For example,
Ptolemy Theorem
The Cosine Law
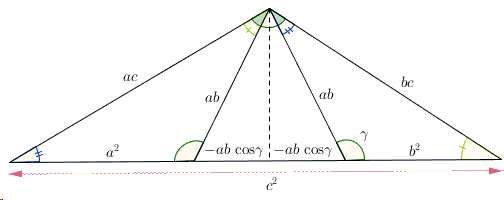
The Cosine Law - II
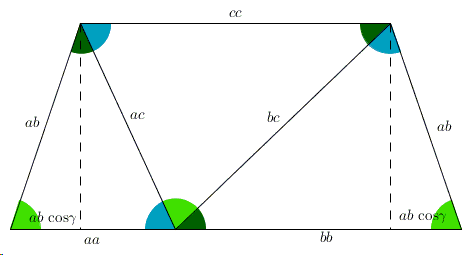
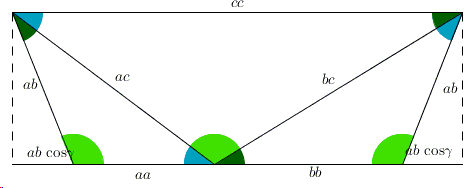
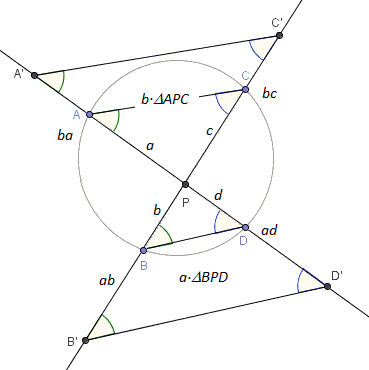
Intersecting Chords Theorem
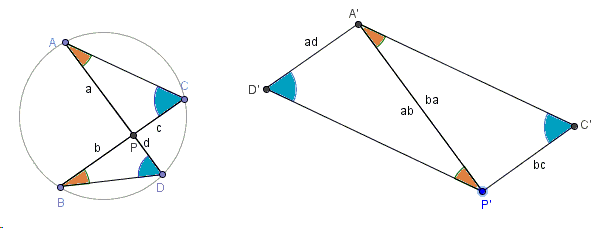
Intersecting Chords Theorem - Unfolded View
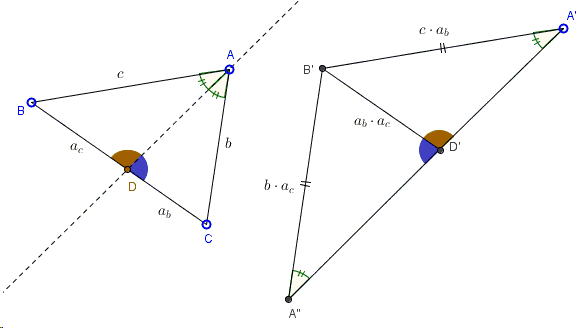
Property of Internal Angle Bisector
References
- E. S. Loomis, The Pythagorean Proposition, NCTM, 1968
![]()
|Contact| |Front page| |Contents| |Geometry| |Up|
Copyright © 1996-2018 Alexander Bogomolny73581198
