Dividing a Segment into Equal Parts by Paper Folding
It is easy to find the midpoint of a side of a square piece of paper by simply folding one of the corners onto an adjacent corner. This done, we can also find 1/3 of the side, as shown below.
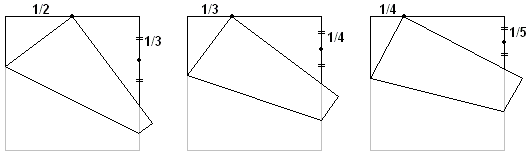
We do not need anything more sophisticated to get 1/4 of the side than finding another midpoint, but, as the second diagram shows, starting with 1/3 of the side we still can get 1/4, and then also 1/5. The procedure is general enough and leads to a successive construction of a 1/k-th of the side for any whole k. To see why this is so, consider the diagram below:
 ,
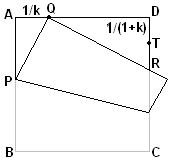where the corner B has been folded onto the point Q, such that AQ = AD/k, for a given k, not necessarily an integer. We shall assume the side of the square to be 1. Let AP = x. Then PQ = 1 - x. The Pythagorean proposition gives
(1 - x)2 - x2 = 1/k2,
from which x = (k2 - 1)/(2k2).
Further, angle PQR = 90°, which implies similarity of right triangles APQ and DQR:
DR/DQ = AQ/AP,
or
| DR | = DQ·AQ/AP |
| | = (1 - 1/k) · 1/k · 2k2/(k2 - 1) |
| | = (k - 1)/k · 1/k · 2k2/(k2 - 1) |
| | = 2/(k + 1). |
For the midpoint T of DR, we get
DT = 1/(k + 1),
which proves the construction.
Remark
After completing this page I have discovered R. J. Lang's online paper where he describes this method as Haga's Construction after Kazuo Haga.
Another procedure known as the crossing diagonal method has a longer history and an exiting story that evolved around 1995.
References
- C. Abbott, What Good Is Proof by Induction Anyway?, Math. Horizons, Sept. 2005, pp. 8-9
- R. J. Lang, Four Problems III, British Origami, no 132, October 1988, pp. 7-11
Paper Folding Geometry
|Front page|
|Contents|
|Store|
|Geometry|
Copyright © 1996-2012 Alexander Bogomolny
|
