Viviani's Theorem: What is it?
A Mathematical Droodle

Explanation

|Activities| |Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny

Viviani's Theorem

The applet attempts to illustrate the following theorem:

The sum of distances of a point inside an equilateral triangle or on one of its sides equals the length of its altitude.

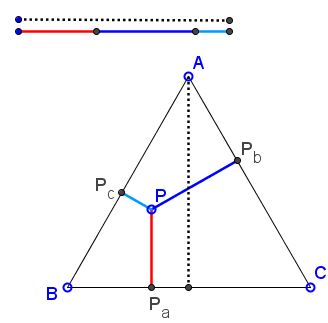
Viviani's theorem

The theorem is named after Vincenzo Viviani (1622-1703).

Let $P_{a},$ $P_{b},$ and $P_{c}$ be the pedal points (projections) of a point $P$ on the side lines $BC,$ $AC,$ and $AB$ of $\Delta ABC.$ Then the theorem claims that

(1)

$h = PP_{a} + PP_{b} + PP_{c},$

where $h$ is the length of the altitudes of $\Delta ABC.$

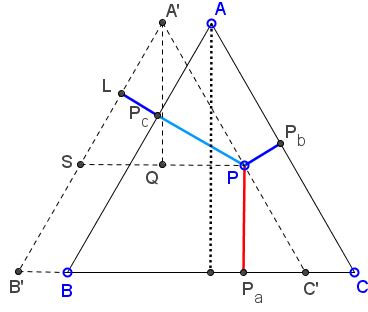
Viviani's theorem, Nelsen's proof

Consider a shifted copy $A'B'C'$ of $\Delta ABC$ such that $P$ lies on $A'C'.$ Let $PS$ be parallel to $BC,$ $Q$ be the foot of the perpendicular from $A'$ onto $PS,$ and $L$ the foot of the perpendicular from $P$ to $A'B',$ as in the applet. Then

$\begin{align} h&= A'Q + PP_{a}\\ &= PL + PP_{a}\\ &= P_{c}L + PP_{c} + PP_{a}\\ &= PP_{b} + PP_{c} + PP_{a}. \end{align}$

A slightly incorrect version of the above appears as a proof without words in [Nelsen, p. 15].

A direct proof is also pretty simple. Let's $[X]$ dennote the area of shape $X.$ As long as point $P$ is not outside $\Delta ABC,$ we have

(2)

$[ABC] = [ABP] + [BCP] + [CAP].$

Let $m$ be the length of a side of $\Delta ABC.$ Then from (2)

$m\cdot h/2 = PP_{c}\cdot m/2 + PP_{a}\cdot m/2 + PP_{b}\cdot m/2,$

wherefrom (1) follows immediately.

Note

  • There is available another proof without words of Viviani's theorem. For you to compare. Also, the theorem extends to equilateral as well as equiangular polygons.

  • There is also a very simple proof by inversion which reduces Viviani's theorem to the identity $AB + BC = AC,$ where $A,$ $B,$ $C,$ are three collinear points with $B$ between $A$ and $C.$

  • Finally, Viviani's theorem follows from a property of isosceles triangles.

References

  1. R. Nelsen, Proofs Without Words, MAA, 1993

Related material
Read more...

  • Equilateral and 3-4-5 Triangles
  • Rusty Compass Construction of Equilateral Triangle
  • Equilateral Triangle on Parallel Lines
  • Equilateral Triangle on Parallel Lines II
  • When a Triangle is Equilateral?
  • Viviani's Theorem (PWW)
  • Viviani in Isosceles Triangle
  • Viviani by Vectors
  • Slanted Viviani
  • Slanted Viviani, PWW
  • Morley's Miracle
  • Triangle Classification
  • Napoleon's Theorem
  • Sum of Squares in Equilateral Triangle
  • A Property of Equiangular Polygons
  • Fixed Point in Isosceles and Equilateral Triangles
  • Parallels through the Vertices of Equilateral Triangle

    • |Activities| |Contact| |Front page| |Contents| |Geometry|

    Copyright © 1996-2018 Alexander Bogomolny

    71945562