Golomb's inductive proof of a tromino theorem
Polyominos were invented by Solomon Golomb, then a 22 year-old student at Harvard, in 1954. A polyomino is a "rook"-connected set of equal squares. (In computer science the kind of connectedness where neighboring squares are required to share an edge is also known as the 4-connectedness. If two squares that share a vertex are also considered neighbors, we get the 8-connectedness.)
Trominos are polyominos that consist of three squares. There are two kinds of trominos: a 3×1 rectangle and an L-shaped piece. A property of the latter is the subject of the following theorem:
Theorem
A unit square has been removed from a 2n×2n board. Prove that the rest of the board can be tiled with L-shaped trominos.
The applet below may help you grasp a proof that is quintessential mathematical induction. You may click inside the applet to "remove" a square or on the "One step" button, to see how, in applet's view, the proof may evolve. Exponent n could be changed with a spin control at the bottom of the applet.
| What if applet does not run? |
|Activities| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
Proof
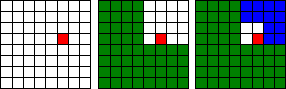
The proof is by induction. For n = 1, the assertion is obvious. With a square removed from a 2×2 board, the remaining part is exactly an L-shaped tromino piece.
Assume the statement true for n = k-1 and let n = k. Draw the center lines of the 2k×2k board. The cut-off square lies in exactly one of the four thus obtained 2k-1×2k-1 boards. We may remove one square from each of the other three boards by placing a tromino at the center of the 2k×2k board. The result is a tromino and four 2k-1×2k-1 boards, each with a square removed - just a situation to apply the inductive hypothesis.
The proof is so simple, its first step was made into a proof without words.
Remark 1
You can test your understanding of Golomb's theorem by trying to tile the board manually.
Remark 2
We may base the last step of the proof on the fact that a tromino can be covered with 4 twice as small copies of itself which makes it a rep-4 tile (a rep-tile variety):
![]()
Thus a 2k×2k board could be looked at as combining one big piece (green) of tromino and a smaller, 2k-1×2k-1 board with a 1×1 square removed.
References
- B. Bollobás, The Art of Mathematics: Coffee Time in Memphis, Cambridge University Press, 2006, #40
- S. Golomb, Two Right Tromino Theorems, in The Changing Shape of Geometry, edited by C. Pritchard, Cambridge University Press, 2003
- R. Nelsen, Proofs Without Words II, MAA, 2000, p. 123
|Activities| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
73512996
