The 80-80-20 Triangle

Several triangles due to their specific properties served as a source for research, wonderment, and a variety of problems. Some, like equilateral, right isosceles, golden, Egyptian, 30-60-90, are very well known. One triangle that deserves more recognition has probably entered mathematical folklore some 100 years ago. Tom Rike of Berkley Mathematical Circles mentions its appearance in the Mathematical Gazette, Volume 11 (1922), p. 173. (His online article also provides additional references.) This is the 80-80-20 (or sometimes 20-80-80) triangle, i.e., the isosceles triangle with the apex angle of 20° and the base angles of 80°.

The original problem gave rise to a few modifications; and each of them has been solved in many, many ways. I'll be adding solutions and perhaps problems related to the original one. Any assistance is welcomed.

This page is to serve as the portal for this undertaking.


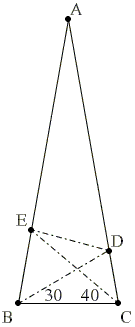
Original problem	60-70 variant	Short segments	Long segments	Isosceles partition

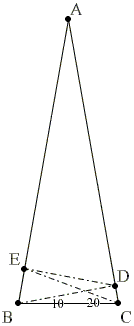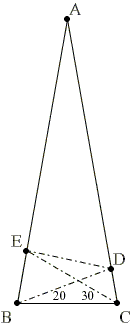
Another partition	40-50 Variant	30-40 variant	20-30 variant	10-20 variant

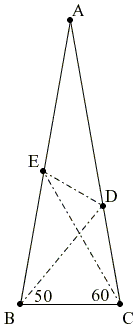
Original problem

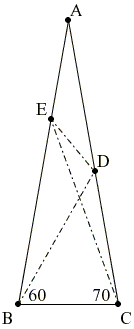
Let ABC be an isosceles triangle (AB = AC) with ∠BAC = 20°. Point D is on side AC such that ∠CBD = 50°. Point E is on side AB such that ∠BCE = 60°. Find the measure of ∠CED.

Solutions

60-70 Variant

Let ABC be an isosceles triangle (AB = AC) with ∠BAC = 20°. Point D is on side AC such that ∠CBD = 60°. Point E is on side AB such that ∠BCE = 70°. Find the measure of ∠CED.

Solutions

Short segments equality

ABC is an isosceles triangle with vertex angle ∠BAC = 20° and AB = AC. Draw ∠BCD = 60°; D lying on AB. Draw an arc with B as center and radius equal to BC. Let this arc cut AC at point E and AB at the point F. Prove that CE = DF.

Solutions

Long segments equality

ABC is an isosceles triangle with vertex angle ∠BAC = 20° and AB = AC. Point E is on AB such that AE = BC. Find the measure of ∠AEC.

Solutions

Partition into adjacent isosceles triangles

The 80-80-20 triangle can be partitioned into isosceles triangle with bases on the legs of the given triangle. For what other apex angles A can isosceles triangle ABC be tessellated with isosceles triangles in a similar manner?

Solutions

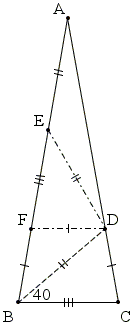
Partition that starts with a base angle bisector

The 80-80-20 triangle can be partitioned in a curious way: let BD, with D on AC, bisect angle B. Then AD = BC + BD.

Solutions

This problem admits an inverse.

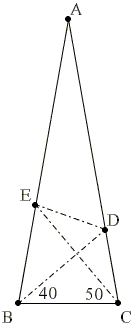
40-50 Variant

Let ABC be an isosceles triangle (AB = AC) with ∠BAC = 20°. Point D is on side AC such that ∠CBD = 40°. Point E is on side AB such that ∠BCE = 50°. Find the measure of ∠CED.

Solutions

30-40 Variant

Let ABC be an isosceles triangle (AB = AC) with ∠BAC = 20°. Point D is on side AC such that ∠CBD = 30°. Point E is on side AB such that ∠BCE = 40°. Find the measure of ∠CED.

Solutions

20-30 Variant

Let ABC be an isosceles triangle (AB = AC) with ∠BAC = 20°. Point D is on side AC such that ∠CBD = 20°. Point E is on side AB such that ∠BCE = 30°. Find the measure of ∠CED.

Solution

10-20 Variant

Let ABC be an isosceles triangle (AB = AC) with ∠BAC = 20°. Point D is on side AC such that ∠CBD = 10°. Point E is on side AB such that ∠BCE = 20°. Find the measure of ∠CED.

Solutions

References

T. Rike, An Intriguing Geometry Problem, Berkeley Math Circle, May 5, 2002.
H. S. M. Coxeter and S. L. Greitzer, Geometry Revisited, MAA, 1967.
R. Honsberger, Four Minor Gems from Geometry, Mathematical Gems II, MAA, 1976.
R. Honsberger, Three Solutions to a Variation on an Old Chestnut, Mathematical Chestnuts from Around the World, MAA, 2001.
C. Knop, Nine Solutions to One Problem, Kvant, 1993, no 6.
R. Leikin, Dividable Triangles - What Are They?, Mathematics Teacher, May 2001, pp. 392-398.
V. V. Prasolov, Essays on Numbers and Figures, MAA, 2000.

71931203