| Manifesto | Bookstore | Contents | Amazon store | Term index | What changed? | Contact | Recommend |
The 80-80-20 Triangle Problem,
|
|
|
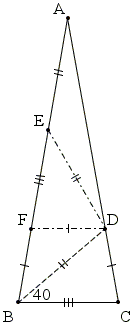
The 80-80-20 triangle can be partitioned in a curious way: let BD, with D on AC, bisect angle B. Then |
Copyright © 1996-2010 Alexander Bogomolny
|
The 80-80-20 triangle can be partitioned in a curious way: let BD, with D on AC, bisect angle B. Then |
|
|
Let F on AB be such that DF||BC and choose E on AB so that
On the other hand, ∠BDC = 180° - 40° - 80° = 60°. Therefore,
ΔBFD is also isosceles because ∠BDF = 180° - 80° - 60° = 40°, such that
Finally, ∠EDF = 80° - 20° = 60° = ∠EDC. We see that triangles BCD and EFD are equal (by SAS), implying
It follows that
| AD | = AF | |
| = AE + EF | ||
| = BD + BC. |
As a follow up, a problem has been posted at the CTK Exchange:
|
In ΔABC, ∠B = 80°. The bisector of angle B meets AC in D such that |
Copyright © 1996-2010 Alexander Bogomolny
| 35699964 |  |
