The 80-80-20 Triangle Problem, 20-30 case
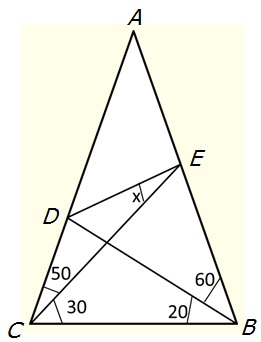
Let $ABC$ be an isosceles triangle $(AB = AC)$ with $\angle BAC = 20^{\circ}.$ Point $D$ is on side $AC$ such that $\angle CBD = 20^{\circ}.$ Point $E$ is on side $AB$ such that $\angle BCE = 30^{\circ}.$ Find the measure of $\angle CED.$
|Contact| |Front page| |Contents| |Geometry| |Up|
Copyright © 1996-2018 Alexander Bogomolny

Let $ABC$ be an isosceles triangle $(AB = AC)$ with $\angle BAC = 20^{\circ}.$ Point $D$ is on side $AC$ such that $\angle CBD = 20^{\circ}.$ Point $E$ is on side $AB$ such that $\angle BCE = 30^{\circ}.$ Find the measure of $\angle CED.$
Below there are a few results by MvG who pointed out to me a discussion at a stackexchange. In all likelihood, there is no rational solution either in degrees, radians, or as a fraction of $\pi.$ However, this remains to be proved.
The angle was found approximately to be:
$x\approx 17.877987144333100702669230434486544610886743725521...^{\circ},$
as a solution of
$1216\cos^{6}x-3264\cos^{4}x+2916\cos^{2}x-867=0.$
It was found in a way typical for third degree equations to involve complex numbers that eventually cancel out:
$\displaystyle x=\arccos\sqrt{ \frac{17}{19}-\frac{1+\sqrt{-3}}{152} \sqrt[3]{\frac{-17+19\sqrt{-3}}2} -\frac{7 (1-\sqrt{-3})}{76 \sqrt[3]{-68+76\sqrt{-3}}}}.$
In terms of sine he equation becomes
$1216\sin^6x - 384\sin^4x + 36\sin^2x - 1=0.$
Without explicit roots the solution was found also in two ways:
$\begin{align}\displaystyle x&=\arctan\frac{2\cos80^{\circ}(2\cos^{2}80^{\circ}-1)(8\cos^{4}80^{\circ}-8\cos^{2}80^{\circ}+1)}{\sin80^{\circ}(32\cos^{6}80^{\circ}-32\cos^{4}80^{\circ}+8\cos^{2}80^{\circ}-1)}\\ x&=\arctan\frac{2\cos80^{\circ}(2\sin^{2}80^{\circ}-1)(8\sin^{4}80^{\circ}-8\sin^{2}80^{\circ}+1)}{\sin80^{\circ}(32\sin^{6}80^{\circ}-64\sin^{4}80^{\circ}+40\sin^{2}80^{\circ}-7)}. \end{align}$
These were obtained this by expressing the construction in terms of these trigonometric functions, then simplifying the result using $sin^{2}+cos^{2}=1.$
What follows is a contribution by Jonathan Lubin:
I think itís sufficient to handle this with coordinate geometry. Iím going to place the lower left vertex of the triangle at the origin, and the lower right vertex at $(1,0)$. Letís name all five of the small triangles making up the figure, starting at the top, triangle $\alpha$. Then, going around the perimeter clockwise, the triangle containing your angle $x$ will be called $\beta$, then $\gamma$ is the upper triangle with a vertex at the lower right vertex of the whole thing, then $\delta$, and finally $\varepsilon$.
So Iíll say that the whole triangle is $\alpha+\beta+\gamma+\delta+\varepsilon$, and any of the smaller ones may be described as the sum (union) of a subset of the five named ones. Letís also name $A$ as the common vertex of $\alpha$, $\beta$, and $\varepsilon$, and $B$ as the common vertex of triangles $\alpha$, $\beta$, and $\gamma$. Whatís crucial to our discussion is the problem of finding the slope of the line segment $\overline{AB}$.
Letís make some preliminary observations. The big triangle is isosceles, having angles of 80 at both vertices on the horizontal axis. (Iím going to omit the degree sign from here on.) Since the angle of 80 shows up again and again, Iím going to use the notation $T=\tan80^{\circ}$, $S=\sin80^{\circ}$, and $C=\cos80^{\circ}$. So we see that the top vertex has coordinates $(\frac12,T/2)$. Notice also that thereís another $(80^{\circ},80^{\circ},20^{\circ})$ isosceles triangle, itís the triangle $\delta+\varepsilon$, which has the point $A$ as the top one of its vertices. So we have similar triangles, and we can get the length $\ell$ of the segment from the origin to $A$. Using leg/base, we get
$\displaystyle \frac{\frac12\sec80^{\circ}}1=\frac1\ell\,,\qquad\ell=2C\,. $
Thus the coordinates of $A$ are $(2C^2,2CS)$.
Now $B$ is at the intersection of the line $Y=X/\sqrt3$, because $\tan30^{\circ}=1/\sqrt3$, and the line of slope $T$ passing through $(1,0)$, so its equation is $Y=-T(X-1)$. Solve these two first for $X$, then for $Y$:
$\displaystyle X=\frac T{T+\frac1{\sqrt3}}\,,\qquad Y=X/\sqrt3=\frac T{1+\sqrt3T}\,. $
From this, the slope $m$ of $\overline{AB}$ is
$\displaystyle \frac{\frac T{1+\sqrt3}-2CS} {\frac{\sqrt3T}{1+\sqrt3T}-2C^2} =\frac{T-2CS(1+\sqrt3T)}{\sqrt3T-2C^2(1+\sqrt3T)}\,, $
which works out numerically to $m=.2147833$. Now we need the angle between this and a line of slope $1/\sqrt3$, so we get
$\displaystyle \tan x=\frac{\frac{1}{\sqrt3}-m}{1+\frac m{\sqrt3}}=\frac{1-\sqrt3m}{\sqrt3+m} \approx .3225670\,, $
which gives $x\approx 17.8779872^{\circ}$. I did all these numerics on my HP15-C !
|Contact| |Front page| |Contents| |Geometry| |Up|
Copyright © 1996-2018 Alexander Bogomolny
73582274
