From one of the solutions to a problem related to the 80-80-20 isosceles triangle, we know that the latter can be decomposed into four isosceles triangles with the bases on the legs of the given triangle.

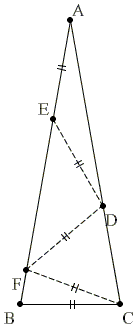
Below, we follow an article by Roza Leikin who considered a generalized problem: which isosceles triangles (defined by, say, their apex angle) possess what she called "Consecutive Isosceles Division"? I'll use the term "Consecutive Isosceles Decomposition", instead, and the same abbreviation, CID.

Solution

Reference

1. R. Leikin, Dividable Triangles — What Are They?, Mathematics Teacher, May 2001, pp. 392–398.

Copyright © 1996-2008 Alexander Bogomolny

For the original 80-80-20 triangle, we found a 4-triangle decomposition into 20-20-140, 40-40-100, 60-60-60, and 80-80-20 triangles. Note that the base angles form an arithmetic sequence 20, 40, 60, 80 (as are the apex angles.)

We shall prove that the same pattern holds for every CID decomposition. Indeed, let P_k-1P_kP_k+1 and P_kP_k+1P_k+1 be two adjacent triangles of such a decomposition, one with base P_k-1P_kP_k+1 = α and the other with the base P_k+1P_kP_k+2 = β, α > β. The difference between the two angles is α - β, obviously.

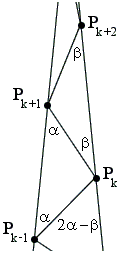
In the next triangle down the diagram, i.e. ΔP_k-2P_k-1P_k, the base P_k-1P_kP_k-2 is found to be

Pk-1PkPk-2 = 180° - (180° - 2α - β) = 2α - β,

with the same difference α - β from the previous base angle α.

Assume that an isosceles triangle ABC (AB = AC) with the apex angle of γ admits an n-term CID. The top triangle has an apex angle of (180° - 2γ) so that the next triangle's base angle is

implying that the difference of the arithmetic sequence of the base angles in the CID is equal γ, the apex angle of ΔABC. The base angle of ΔABC is clearly (180° - γ)/2. For the n-term arithmetic sequence of the base angles we thus have

from which

Note that such an angle is half the central angle between two consecutive vertices of a regular (2n+1)-gon.

As we've seen, for γ = 20°, i.e. for the 80-80-20 triangle, 2n + 1 = 9 and n = 4. For n = 1, γ = 60°, as an equilateral triangle is its own 1-term decomposition. For n = 2, γ = 180°/5 = 36° leading to a golden triangle 72-72-36. Next comes the triangle with the non-constructible apex of π/7.

Copyright © 1996-2008 Alexander Bogomolny