Common Centroids Lead to Equilateral Triangle
What is this about?
Source
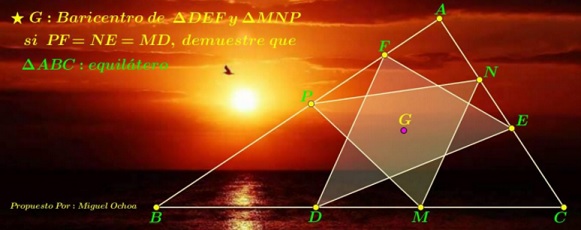
Problem
In $\Delta ABC,\;$ $D,M\in BC,\;$ $E,N\in AC,\;$ $F,P\in AB.\;$ Also, $DM=EN=FP$ and it is known that triangles $DEF\;$ and $MNP\;$ have a common centroid at $G.\;$
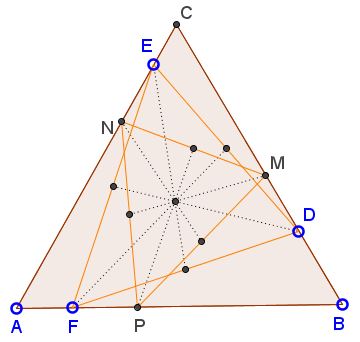
Prove that $\Delta ABC\;$ is equilateral.
Solution 1
We choose $A=0,\;$ $B=b,\;$ and $C=c.\;$ Obviously $b\ne c\ne 0\ne b.\;$ Further, $\displaystyle\frac{b}{c}=\frac{B-A}{C-A}\;$ is not a real number. Let's fix the order of $B,D,MC\;$ on the side $BC.\;$ Then there are real numbers $\alpha,\mu,\;$ with $0\lt\mu\alpha\lt 1\;$ such that $D=\alpha B+(1-\alpha )C\;$ and $M=\mu B+(1-\mu)C,\;$ i.e., $D=\alpha b+(1-\alpha )c\;$ and $=\mu b+(1-\mu)c.\;$ Similarly, $E=\beta c,\;$ $N=\nu c,\;$ $0\lt \nu\lt\beta\lt 1,\;$ and $F=(1-\gamma)b,\;$ $P=(1-\rho)b,\;$ $0\lt\rho\lt\gamma\lt 1.\;$
Since the triangles $DEF\;$ and $MNP\;$ have the same centroid, $D+E+C=M+N+F,\;$ implying
$(1+\alpha-\gamma)b+(1+\beta-\alpha)c=(1+\mu-\rho)b+(1+\nu-\mu)c,$
from which $1+\alpha-\gamma=1+\mu-\rho\;$ and $1+\beta-\alpha=1+\nu-\mu\;$ because $\displaystyle\frac{b}{c}\;$ is not real. It follows that $\alpha-\gamma=\mu-\rho\;$ and $\beta-\alpha=\nu-\mu\;$ and, with an rearrangement of the terms,
$\rho-\gamma=\alpha-\mu=\beta-\nu.$
On the other hand, $MD=(\alpha-\mu)BC,\;$ $NE=(\beta-\nu)CA,\;$ and $PF=(\gamma-\rho)AB.\;$ Combining all that we get $AB=BC=CA.$
Solution 2
Centroid $G\;$ of any three points, say, $X_1,X_2,X_3\;$ has the property that $GX_1+GX_2+GX_3=0.\;$ Indeed, centroid is defined by $\displaystyle G=\frac{X_1+X_2+X_3}{3},\;$ or $3G=X_{1}+X_{2}+X_{3},\;$ i.e., $(X_1-G)+(X_2-G)+(X_3-G)=0,\;$ or $GX_1+GX_2+GX_3=0.\;$
If, in addition, the centroid coincides with the circumcenter, i.e., if $GX_1=GX_2=GX_3\;$ then $\Delta X_1X_2X_3\;$ is equilateral. This is because, $GX_1=GX_2=GX_3\;$ makes the medians in $\Delta_1X_2X_3\;$ equal so that the triangle formed by the medians - the median triangle - is equilateral. But the halves of the sides of $\Delta_1X_2X_3\;$ are the medians of the triangle formed by $GX_1,GX_2,GX_3\;$ and are, therefore, equal if the latter are. One of the consequences of that is the fact that angles $X_1GX_2,\;$ $X_2GX_3,\;$ $X_3GX_1\;$ all are $120^{\circ}.$
We are given that triangles $DEF\;$ and $MNP\;$ share the centroid. If so, $D+E+F=M+N+P,\;$ or $DM+EN+FP=0.\;$ It is also given that $DM=EN=FP.\;$ From the discussion above the angles between $DM,EN,\;$ $EN,FP,\;$ and $FP,DM\;$ are all $120^{\circ}\;$ which exactly means that $\Delta ABC\;$ is equilateral.
Solution 3
Given three not pairwise collinear vectors $\mathbf{a},\;$ $\mathbf{b},\;$ $\mathbf{c}\;$ and three real numbers $\alpha,\beta,\gamma\;$ such that
$\mathbf{a}+\mathbf{b}+\mathbf{c}=\mathbf{0}\;$ and
$\alpha\mathbf{a}+\beta\mathbf{b}+\gamma\mathbf{c}=\mathbf{0}\;$
Then $\alpha=\beta=\gamma.$
Indeed, from the above it follows that $(\beta-\alpha)\mathbf{b}+(\gamma-\alpha)\mathbf{c}=\mathbf{0}.\;$ But, since $\mathbf{b}\;$ and $\mathbf{c}\;$ are not collinear, they are independent, implying that $\beta-\alpha=\gamma-\alpha=0.\;$
Returning to the problem at hand, as we have already seen, since triangles $DEF\;$ and $MNP\;$ share the centroid, $\overrightarrow{DM}+\overrightarrow{EN}+\overrightarrow{FP}=\mathbf{0}.\;$ But also $\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CA}=\mathbf{0}.\;$ Obviously, $\overrightarrow{DM}=\alpha\overrightarrow{AB},\;$ $\overrightarrow{EN}=\beta\overrightarrow{BC},\;$ and $\overrightarrow{FP}=\gamma\overrightarrow{CA}\;$ which implies $\alpha=\beta=\gamma.\;$ It follows that if $DM=EN=FP$ then necessarily $AB=BC=CA.$
Acknowledgment
The problem due to Miguel Ochoa Sanchez has been posted by Leo Giugiuc at the CutTheKnotMath facebook page, with the solution (Solution 1) by Claudia Nanuti, Diana Trailescu, Dan Sitaru and Leo Giugiuc communicated privately. Solution 2 is by Imad Zak. Solution 3 has been inspired by that of Imad Zak.
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73574849
