Equal Areas in Equilateral Triangle: What is it about?
A Mathematical Droodle
Explanation
|Activities|
|Contact|
|Front page|
|Contents|
|Geometry|
|Store|
Copyright © 1996-2012 Alexander Bogomolny
The applet purports to illustrate one of the many properties of an equilateral triangle.
Let M be a point inside an equilateral triangle ABC, with pedal points A', B', and C', as shown. The lines joining M to the six points A, B, C, A', B', C' split the triangle into six smaller ones. The applet suggests that
| (1) |
Area(AMB') + Area(BMC') + Area(CMA') = Area(A'MB) + Area(B'MC) + Area(C'MA).
|
(I am grateful to Manuel Silva from Portugal for bringing this problem to my attention.)
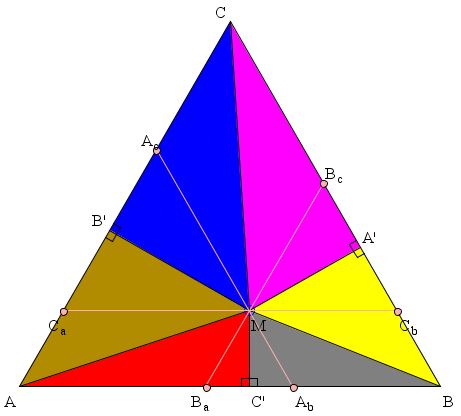
As in a sister problem, Draw AbAc||BC, BaBc||AC, and CaCb||AB. The three lines split ΔABC into three parallelograms and three smaller equilateral triangles. The three parallelograms are divided by the diagonals joining M to the vertices A, B, C into equal parts, whereas the three equilateral triangles are divided into equal parts by the lines joining M to the pedal points A', B', C'. So, for a proof, one only needs to rearrange the areas in (1).
|Activities|
|Contact|
|Front page|
|Contents|
|Geometry|
|Store|
Copyright © 1996-2012 Alexander Bogomolny
|
