A Circle Rolling in an Equilateral Triangle
What is this about?
A Mathematical Droodle
| Buy this applet What if applet does not run? |
|Activities| |Contact| |Front page| |Contents| |Geometry| |Store|
Copyright © 1996-2015 Alexander BogomolnyThe applet may suggest the following statement:
Given an equilateral triangle ABC and a circle Γ tangent to BC, with the radius equal to the altitude of ΔABC. Circle Γ may roll along BC between two extreme positions when it contains either B or C.
1. For every position, it meets AB and AC in D and E, respectively. Prove that, regardless of the position of &Gamma, arc DE is exactly 60°.
2. The lens obtained by reflecting that arc in the chord DE is always located inside ΔABC.
| Buy this applet What if applet does not run? |
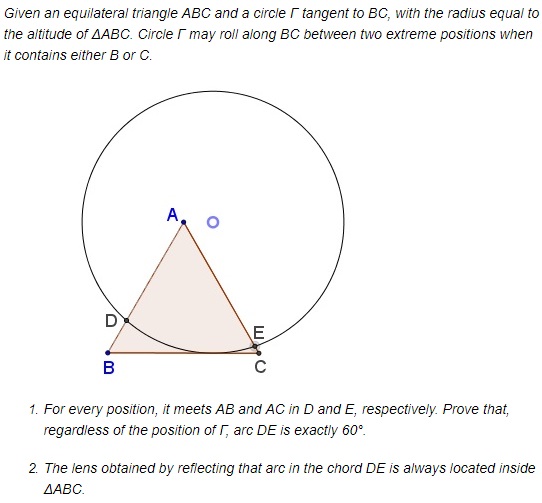
Proof
Let B' be the reflection of C in A and C' that of B. Let λ be the line through A parallel to BC. We see that ΔAB'C' is the symmetric image of ΔABC in λ and so are the two halves of circle Γ cut off by λ. It follows that the two arcs cut off by Γ inside the two triangles are equal.
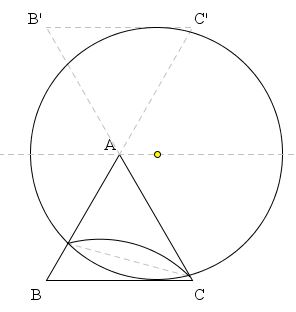
On the other hand, ∠BAC formed by two lines BC' and B'C could be looked at as formed by two intersecting chords. It therefore equals half the sum of the two arcs and, since they are equal, to either of them. But
At the extreme positions of Γ the angle formed by DE and BC is 30° and DE serves as a bisector of either ∠B or ∠C. In-between the angle is less than 30°. This angle is equal to the angle formed by DE with the upper border of the lens which then is also less than 30°. But this exactly means that the upper arc crosses neither AB nor AC.
Obviously, the lens fit snuggly in the equilateral triangle and may rotate there always touchingits sides. The lens is a simplified analog of shapes of constant width
References
- D. O. Shklyarsky, N. N. Chentsov, I. M. Yaglom, Selected Problems and Theorems from Elementary Mathematics, Geometry, 1952 (in Russian)
|Activities| |Contact| |Front page| |Contents| |Geometry| |Store|
Copyright © 1996-2015 Alexander Bogomolny| 49552162 |
