Equilateral Triangles on Sides of a Parallelogram III
What is this about?
Problem
In $\Delta ABC,\;$ $M\in BC,\;$ $B_1\in AC,\;$ $C_1\in AB;\;$ $B_1M\parallel AB,\;$ $C_1M\parallel AC.\;$ Triangles $AB_1Q\;$ and $AC_1K\;$ area equilateral. $N\;$ is the intersection of $MQ\;$ with $AB,\;$ $P\;$ is the intersection of $KM\;$ with $AC.$
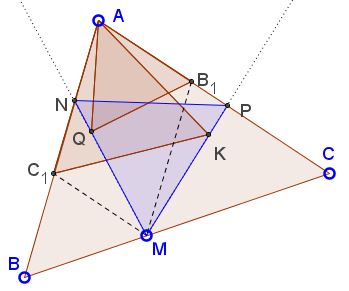
Prove that $\Delta MNP\;$ is equilateral.
Proof
Let $D,\;$ $E,\;$ $F,\;$ be the midpoints of $AQ,\;$ $AK,\;$ and $B_1C_1,\;$ respectively.
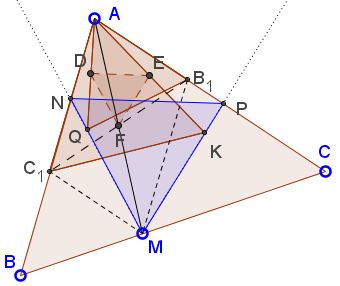
From the Fundamental Theorem of Directly Similar Figures, $\Delta DEF\;$ is equilateral. In addition, since $AC_1MB_1\;$ is a parallelogram, $F\;$ is the midpoint of $AM.\;$ By a homothety with center $A,\;$ $\Delta QKM\;$ is also equilateral.
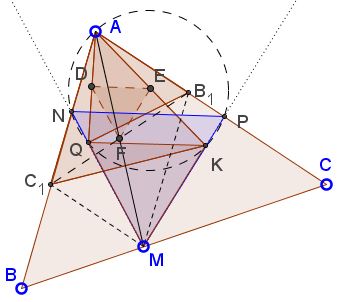
By angle chasing, points $A,\;$ $N,\;$ $Q,\;$ $K,\;$ and $P\;$ are concyclic. Indeed, by the construction, $\angle KAN=60^{\circ},\;$ while $\angle KQN\;$ may be either $60^{\circ}\;$ or $180^{\circ},\;$ depending on whether $Q\;$ falls inside or outside $\Delta ABC.\;$ This makes points $A,\;$ $N,\;$ $Q,\;$ and $K,\;$ concyclic. Similarly, points and $A,\;$ $P,\;$ $Q,\;$ and $K,\;$ are also concyclic so that all five lie on circle $(AKQ).\;$ It follows that $KQ\parallel NP,\;$ making $\Delta MNP\;$ equilateral.
Remark
Points $B\;$ and $C\;$ play rather superficial roles in the formulation of the problem. A more direct setting would start with a parallelogram $AC_1MB_1$ or even $\Delta AB_1C_1.$
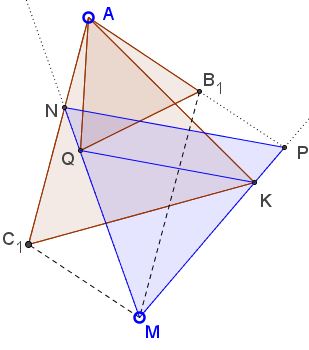
Indeed, construction of equilateral triangles on the sides of a parallelogram has been previously looked into and - in the present setting - would show that $\Delta QKM\;$ is equilateral. Furthermore, the above problem repeats Paul Yiu's construction of equilateral triangle related to a given parallelogram, but offers an independent proof of that result.
Acknowledgment
The problem and the solution are by Thanh Oai Dao.
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73581292
