Problem 2, the 36th IMO (1995)
Problem
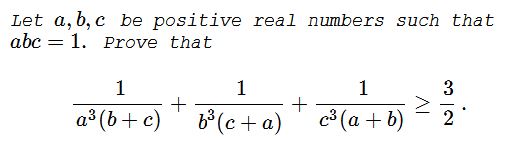
Solution 1
Let's make a substitution $a=\displaystyle\frac{1}{x},\,$ $b=\displaystyle\frac{1}{y},\,$ $c=\displaystyle\frac{1}{z}.\,$ Still, $xyz=1\,$ and the inequality becomes
$\displaystyle \frac{x^3yz}{y+z}+\frac{y^3zx}{z+x}+\frac{z^3xy}{x+y}\overset{xyz=1}{=}\frac{x^2}{y+z}+\frac{y^2}{z+x}+\frac{z^2}{x+y}\ge\frac{3}{2}.$
If $S=\displaystyle\frac{x^2}{y+z}+\frac{y^2}{z+x}+\frac{z^2}{x+y}\,$ then, by the Cauchy-Schwarz inequality,
$[(y+z)+(z+x)+(x+y)]\cdot S\ge (x+y+z)^2,$
implying $\displaystyle S\ge\frac{x+y+z}{2}\ge\frac{3\sqrt[3]{xyz}}{2}=\frac{3}{2},\,$ with equality when $x=y=z=1,\,$ i.e., for $a=b=c=1.$
Solution 2
Starting with the same substitution as in Solition 1, we prove
$\displaystyle\frac{x^2}{y+z}+\frac{y^2}{z+x}+\frac{z^2}{x+y}\ge\frac{3}{2}$
simply with Bergström's inequality, followed by Cauchy-Schwarz inequality inequality as above.
Solution 3
Consider point $\displaystyle P=\left(\frac{1}{(a^3(b+c))^{1/2}},\frac{1}{(b^3(c+a))^{1/2}},\frac{1}{(c^3(a+b))^{1/2}}\right)\in\mathbb{R}^3\,$ and plane $\mathcal{P} :\,(ab+ac)^{1/2}x+(bc+ba)^{1/2}y+(ca+cb)^{1/2}z=0.\,$ Then $O(0,0,0)\in\mathcal{P}.\,$ Denote by $D(P,O)\,$ the distance from $P\,$ to $O\,$ and by $D(P,\mathcal{P})\,$ the distance from $P\,$ to $\mathcal{P},\,$ respectively. It's easy to see that
$\displaystyle D^2(P,O)=\frac{1}{a^3(b+c)}+\frac{1}{b^3(c+a)}+\frac{1}{c^3(a+b)}$
and, by using the distance formula from a point to a plane (and omitting some of the tedious algebra here), we get
$\displaystyle\begin{align} D^2(P,\mathcal{P})&=\frac{\displaystyle\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)^2}{2(ab+bc+ca)}\\ &=\frac{ab+bc+ca}{2}\\ &\ge\frac{3(ab\cdot bc\cdot ca)^{1/3}}{2}=\frac{3}{2}. \end{align}$
Since $D^2(P,O)\ge D^2(P,\mathcal{P}),\,$ the result follows.
Solution 4
First, let $p=a+b+c,\,$ $q=ab+bc+ca,\,$ $r=abc.\,$ By the AM-GM inequality $q\ge 3\,(1).\,$ Further, $q^2\ge 3pr=3p,\,$ so that $3p\le q^2\,(2).$
Rewrite the given inequality as
$\displaystyle E=\sum_{cycl}\frac{b^3c^3}{b+c}\ge\frac{3}{2}.$
$\displaystyle\begin{align} 3\cdot E\cdot 2p &= E\cdot ((b+c)+(c+a)+(a+b))(1+1+1)\\ &\overset{Hölder}{\ge}(bc+ca+ab)^3, \end{align}$
implying $\displaystyle E\ge\frac{q^3}{3(2p)}.\,$ With (2), we get $\displaystyle E\ge\frac{q^3}{2q^2}=\frac{q}{2}.\,$ Now, via (1),
$\displaystyle E=\frac{q}{2}\ge\frac{3}{2}.$
Equality for $a=b=c=1.$
Acknowledgment
I came up to considering this problem on receiving Sidney Kung's communication on applications of the Cauchy-Schwarz inequality. Solution 3 is a part of this communication. Solution 1 is from The IMO Compendium by Dusan Djukic et al.; Solution 4 is by Imad Zak.
Aditional solutions are available online in an article Several proofs and generalizations of a fractional inequality with constraints by Fuhua Wei and Shanhe Wu.
Inequalities with the Product of Variables as a Constraint
- An Application of Schur's Inequality II $\left(\sum (x^4+y^3+z) \ge \sum \left(\frac{x^2+y^2}{z}\right)+3\right)$
- Problem 1 From the 2016 Pan-African Math Olympiad $\left(\displaystyle \sum_{cycl}\frac{1}{(x+1)^2+y^2+1}\le\frac{1}{2}\right)$
- A Cyclic But Not Symmetric Inequality in Four Variables $\left(\displaystyle 5(a+b+c+d)+\frac{26}{abc+bcd+cda+dab}\ge 26.5\right)$
- Problem 2, the 36th IMO (1995) $\left(\displaystyle \frac{1}{a^3(b+c)}+\frac{1}{b^3(c+a)}+\frac{1}{c^3(a+b)}\ge\frac{3}{2}\right)$
- An Inequality with Two Cyclic Sums $\left(\displaystyle \sum_{cycl}(a+\sqrt[3]{a}+\sqrt[3]{a^2})\ge 9\sum_{cycl}\frac{1}{1+\sqrt[3]{b^2}+\sqrt[3]{c}}\right)$
- The Roads We Take $(x(x-3(y+z))^2+(3x-(y+z))^2(y+z)\ge 27)$
- Long Huynh Huu's Inequality and Solution $\left(\displaystyle \sum_{i=1}^n\arctan x_i\le (n-1)\frac{\pi}{2}\right)$
- An Inequality with Integrals $\left(\Omega=\int_0^u\frac{u^4+7x^3-25x^2+37x+4}{x^4-3x^3+5x^2-3x+4}dx,\;\Omega(a)+\Omega(b)+\Omega(C)\ge3+5\ln\prod_{cycl}(1+a^2)\right)$
- An Inequality with Cycling Sums $\left(\displaystyle\sum_{cycl}(x^4+y^3+z)\ge \sum_{cycl}\frac{x^2+y^2}{z}+3\right)$
- Two Products: Constraint and Inequality $\left(\displaystyle\prod_{k=1}^n(1+a_k)\ge 2^n\right)$
- Leo Giugiuc's Cyclic Inequality with a Constraint $\left(\displaystyle a^3+b^3+c^3+\frac{16}{(a+b)(b+c)(c+a)}\ge 5\right)$
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73578546
