Long Huynh Huu's Inequality and Solution

Problem

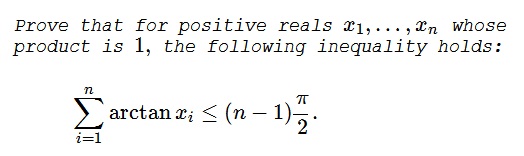
A Simplified Version of Leo Giugiuc's Inequality from the AMM

Solution

Lemma

Let $x_1,...,x_n$ be positive integers, $n \geq 1$. Then

(1)

$\displaystyle \sum_{i=1}^n \arctan(x_i) \geq \arctan(x_1...x_n)$

Proof of Lemma

WLOG, $x_1\geq ... \geq x_n$.

(2)

$\displaystyle \sum_{i=1}^n \arctan(x_i) \geq \arctan(x_1) \geq \arctan(\sqrt[n]{x_1...x_n}),$

as the maximal value $x_1$ is greater than (or equal to) the geometric mean of all $x_i$.

Case 1: $\mathbf{\displaystyle \prod_{i=1}^n x_i \leq 1}$

In this case $\sqrt[n]{\prod_i x_i} \geq \prod_i x_i$, so the claim follows from (1) and monotonicity of $\arctan$.

Case 2: $\mathbf{\displaystyle \prod_{i=1}^n x_i \gt 1}$

If $x_2 \geq 1$, then

$\displaystyle \arctan(x_1) + \arctan(x_2) \geq \frac{\pi}{4} +\frac{\pi}{4} = \frac{\pi}{2} > \arctan(x_1...x_n).$

Otherwise if $x_1 \gt 1$ and $x_2 \lt 1$, then

$\displaystyle x_2 \gt \prod_{i=2}^{n} x_i \gt \frac{1}{x_1}.$

and hence

$\displaystyle\begin{align} \arctan(x_1) + \arctan(x_2) &\gt \arctan(x_1) + \arctan(1/x_1)\\ &= \frac{\pi}{2} \gt \arctan(x_1...x_n). \end{align}$

In any case, the claim follows.

Corollary,

Using $\displaystyle \arctan(1/x_i)=\frac{\pi}{2} - \arctan(x_i)$ we get

$\displaystyle \begin{align} &\sum_{i=1}^n \arctan(1/x_i) \geq \arctan\left(\frac{1}{x_1...x_n}\right)\\ &\qquad\qquad\iff n\frac{\pi}{2} \geq \sum_{i=1}^n \arctan(x_i) +\arctan\left(\frac{1}{x_1...x_n}\right) \end{align}$

Acknowledgment

This problem was posed on twitter and solved by Long Huynh Huu.

Inequalities with the Product of Variables as a Constraint

An Application of Schur's Inequality II $\left(\sum (x^4+y^3+z) \ge \sum \left(\frac{x^2+y^2}{z}\right)+3\right)$
Problem 1 From the 2016 Pan-African Math Olympiad $\left(\displaystyle \sum_{cycl}\frac{1}{(x+1)^2+y^2+1}\le\frac{1}{2}\right)$
A Cyclic But Not Symmetric Inequality in Four Variables $\left(\displaystyle 5(a+b+c+d)+\frac{26}{abc+bcd+cda+dab}\ge 26.5\right)$
Problem 2, the 36th IMO (1995) $\left(\displaystyle \frac{1}{a^3(b+c)}+\frac{1}{b^3(c+a)}+\frac{1}{c^3(a+b)}\ge\frac{3}{2}\right)$
An Inequality with Two Cyclic Sums $\left(\displaystyle \sum_{cycl}(a+\sqrt[3]{a}+\sqrt[3]{a^2})\ge 9\sum_{cycl}\frac{1}{1+\sqrt[3]{b^2}+\sqrt[3]{c}}\right)$
The Roads We Take $(x(x-3(y+z))^2+(3x-(y+z))^2(y+z)\ge 27)$
Long Huynh Huu's Inequality and Solution $\left(\displaystyle \sum_{i=1}^n\arctan x_i\le (n-1)\frac{\pi}{2}\right)$
An Inequality with Integrals $\left(\Omega=\int_0^u\frac{u^4+7x^3-25x^2+37x+4}{x^4-3x^3+5x^2-3x+4}dx,\;\Omega(a)+\Omega(b)+\Omega(C)\ge3+5\ln\prod_{cycl}(1+a^2)\right)$
An Inequality with Cycling Sums $\left(\displaystyle\sum_{cycl}(x^4+y^3+z)\ge \sum_{cycl}\frac{x^2+y^2}{z}+3\right)$
Two Products: Constraint and Inequality $\left(\displaystyle\prod_{k=1}^n(1+a_k)\ge 2^n\right)$
Leo Giugiuc's Cyclic Inequality with a Constraint $\left(\displaystyle a^3+b^3+c^3+\frac{16}{(a+b)(b+c)(c+a)}\ge 5\right)$

71532365