An Inequality with Two Cyclic Sums

Problem

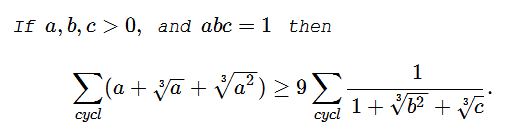
Solution

Let $\sqrt[3]{a}=x,\,$ $\sqrt[3]{b}=y,\,$ $\sqrt[3]{c}=z.\,$ Then still $xyz=1,\,$ $x,y,z\gt 0.\,$

By the Cauchy-Schwarz inequality,

$(1+y^2+z)(x^2+1+z)\ge (x+y+z)^2\ge 3^2=9,$

implying $\displaystyle \frac{9}{1+y^2+z}\le x^2+1+z.\,$ Similarly, $\displaystyle \frac{9}{1+z^2+x}\le y^2+1+x\,$ and $\displaystyle \frac{9}{1+x^2+y}\le z^2+1+y.\,$ Adding the three gives,

$\displaystyle \begin{align} 9\sum_{cycl}\frac{1}{1+y^2+x}&\le 3+\sum_{cycl}x+\sum_{cycl}x^2\\ &\le\sum_{cycl}x^3+\sum_{cycl}x+\sum_{cycl}x^2\\ &=\sum_{cycl}a+\sum_{cycl}\sqrt[3]{a}+\sum_{cycl}a^2\\ &=\sum_{cycl}(a+\sqrt[3]{b^2}+c). \end{align}$

and this is the required inequality.

Acknowledgment

This problem from the Romanian Mathematical Magazine has been kindly posted at the CutTheKnotMath facebook page by Dan Sitaru. The above solution is by Nguyen Tien Lam.

Inequalities with the Product of Variables as a Constraint

An Application of Schur's Inequality II $\left(\sum (x^4+y^3+z) \ge \sum \left(\frac{x^2+y^2}{z}\right)+3\right)$
Problem 1 From the 2016 Pan-African Math Olympiad $\left(\displaystyle \sum_{cycl}\frac{1}{(x+1)^2+y^2+1}\le\frac{1}{2}\right)$
A Cyclic But Not Symmetric Inequality in Four Variables $\left(\displaystyle 5(a+b+c+d)+\frac{26}{abc+bcd+cda+dab}\ge 26.5\right)$
Problem 2, the 36th IMO (1995) $\left(\displaystyle \frac{1}{a^3(b+c)}+\frac{1}{b^3(c+a)}+\frac{1}{c^3(a+b)}\ge\frac{3}{2}\right)$
An Inequality with Two Cyclic Sums $\left(\displaystyle \sum_{cycl}(a+\sqrt[3]{a}+\sqrt[3]{a^2})\ge 9\sum_{cycl}\frac{1}{1+\sqrt[3]{b^2}+\sqrt[3]{c}}\right)$
The Roads We Take $(x(x-3(y+z))^2+(3x-(y+z))^2(y+z)\ge 27)$
Long Huynh Huu's Inequality and Solution $\left(\displaystyle \sum_{i=1}^n\arctan x_i\le (n-1)\frac{\pi}{2}\right)$
An Inequality with Integrals $\left(\Omega=\int_0^u\frac{u^4+7x^3-25x^2+37x+4}{x^4-3x^3+5x^2-3x+4}dx,\;\Omega(a)+\Omega(b)+\Omega(C)\ge3+5\ln\prod_{cycl}(1+a^2)\right)$
An Inequality with Cycling Sums $\left(\displaystyle\sum_{cycl}(x^4+y^3+z)\ge \sum_{cycl}\frac{x^2+y^2}{z}+3\right)$
Two Products: Constraint and Inequality $\left(\displaystyle\prod_{k=1}^n(1+a_k)\ge 2^n\right)$
Leo Giugiuc's Cyclic Inequality with a Constraint $\left(\displaystyle a^3+b^3+c^3+\frac{16}{(a+b)(b+c)(c+a)}\ge 5\right)$

71547100