An Application of Cauchy-Schwarz Inequality
Sidney H. Kung
Cupertino, CA
December, 2016
Cauchy-Schwarz Inequality
Let $\mathbf{s}=\{s_1, s_2, \ldots, s_n\}\,$ and $\mathbf{t}=\{t_1,t_2,\ldots,t_n\}\,$ be two sequences of real numbers, then
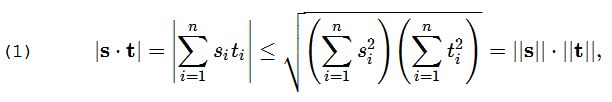
with equality if and only if the two sequences are proportional,i.e., there is a constant $\lambda\,$ such that, say, $\mathbf{s}=\lambda\mathbf{t}.\,$
(The Cauchy-Schwarz inequality has been proved elsewhere.)
Distance in $\mathbb{R}^n$
The distance between two points $P_1,P_2\in\mathbb{R}^n,\,$ $P_k=(x_{k1},x_{k2},\ldots,x_{kn}),\,$ $k=1,2,\,$ is defined by $\displaystyle |P_1P_2|=\sqrt{\sum_{i=1}^n(x_{2i}-x_{1i})^2}.$
Finding the distance from point $P_0=(x_{01},x_{02},\ldots,x_{0n})\,$ to the hyperplane $\displaystyle\mathcal{P}:\,\sum_{i=1}^na_ix_i+b=0,\,$ is equivalent to finding the minimum of the function
$f(x_1,x_2,\ldots,x_n)=\displaystyle\sqrt{\sum_{k=1}^n(x_i-x_{0i})^2},$
subject to the condition $\mathbf{x}=(x_1,\ldots,x_n)\in\mathcal{P}.\,$ Define $\mathbf{u}=\mathbf{x}-\mathbf{x}_0.\,$ Then the problem is equivalent to finding the minimum of $\displaystyle F(u_1,\ldots,u_n)=\sqrt{\sum_{i=1}^nu_i^2},\,$ subject to the condition
$\displaystyle\sum_{i=1}^ka_i(u_i+x_{0i})+b=0.$
Note that $\displaystyle\left|\sum_{i=1}^na_ix_{0i}+b\right|=\left|\sum_{i=1}^na_i(x_{i}-u_i)+b\right|=\left|\sum_{i=1}^na_iu_{i}\right|.$
By applying (1) then, $\displaystyle\left|\sum_{i=1}^na_ix_{0i}+b\right|\le ||\mathbf{a}||\cdot ||\mathbf{u}||,\,$ so that
(2)
$\displaystyle ||\mathbf{u}||=\sqrt{\sum_{i=1}^nu_i^2}\ge\frac{\displaystyle\left|\sum_{i=1}^na_ix_{0i}+b\right|}{\displaystyle\sum_{i=1}^na_i^2}=\frac{|\mathbf{a}\cdot\mathbf{x}_0+b|}{||\mathbf{a}||}.$
Thus, the distance from $P_0\,$ to $\mathcal{P}\,$ is
(3)
$\displaystyle D=\frac{\displaystyle\left|\sum_{i=1}^na_ix_{0i}+b\right|}{\displaystyle\sum_{i=1}^na_i^2}=\frac{|\mathbf{a}\cdot\mathbf{x}_0+b|}{||\mathbf{a}||}.$
(This is a generalization of the formula for the distance from a point to a line, covered elsewhere.)
For (2), equality holds if and only if $\mathbf{u}=\lambda\mathbf{a}.\,$ Substituting that into (3) we find $\lambda :$
(4)
$\displaystyle\lambda=-\frac{\displaystyle\sum_{i=1}^na_ix_{0i}+b}{\displaystyle\sum_{i=1}^na_i^2}=-\frac{\mathbf{a}\cdot\mathbf{x}_0+b}{||\mathbf{a}||^2}.$
Examples
Find the distance $D\,$ from $P=(1,1,-5)\,$ to the plane $12x+13y+5z+2=0.\,$ Find the coordinates of the foot of the perpendicular from $P\,$ to the plane.
From (3), $D=\displaystyle\frac{|12\cdot 1+13\cdot 1+5\cdot (-5)+2|}{\sqrt{12^2+13^2+(-5)^2}}=\frac{\sqrt{2}}{13}.$
From (4), $\displaystyle\lambda=-\frac{2}{12^2+13^2+5^2}=-\frac{1}{169}.\,$ Since $\mathbf{u}=\mathbf{x}-\mathbf{x}_0\,$ and $\lambda\mathbf{a}=\mathbf{x}-\mathbf{x}_0,\,$ we get, as can be easily verified,
$\displaystyle \mathbf{x}=\left(\frac{157}{169},\frac{156}{169},-\frac{850}{169}\right).$
Given $f,g,h\in\mathbb{R}^{+},\,$ and $fgh=1.\,$ Prove that $\displaystyle\frac{1}{f^3(g+h)}+\frac{1}{g^3(h+f)}+\frac{1}{h^3(f+g)}\ge\frac{3}{2}.$
This is problem #2 from the Thirty-Sixth IMO (1995). It has multiple solutions and is considered on a separate page.

|Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny
73518720
