A Property of Right Trapezoids
The following statement has been communicated by Sohail Farhangi:
Given right trapezoid \(ABCD\) with right angles at \(A\) and \(B\). Let circle \(C(M)\) with \(CD\) as diameter intersect \(AB\) in \(F\) and \(H\). Then the perpendicular from \(A\) to \(DF\) and the perpendicular from \(B\) to \(CF\) meet on \(CD\).
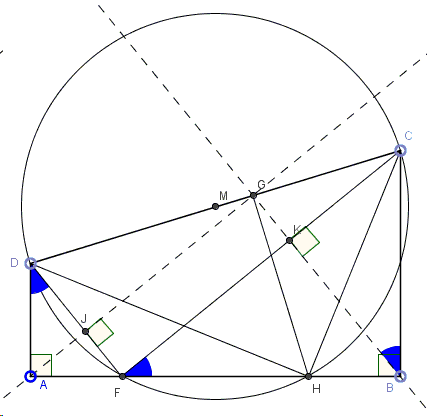
The applet below serves a dynamic illustration
Given right trapezoid \(ABCD\) with right angles at \(A\) and \(B\). Let circle \(C(M)\) with \(CD\) as diameter intersect \(AB\) in \(F\) and \(H\). Then the perpendicular from \(A\) to \(DF\) and the perpendicular from \(B\) to \(CF\) meet on \(CD\).

Proof
Let \(K\) and \(G\) denote the intersections of the perpendicular from \(B\) to \(CF\) with \(CF\) and \(CD\), respectively. Since \(\angle CFD\) subtends in \(C(M)\) diameter \(CD\), it is right: \(\angle CFD=90^{\circ}\). This makes triangles \(CDF\) and \(CGK\) similar, implying the proportion \(\displaystyle\frac{CG}{DG}=\frac{CK}{FK}\). Noting that the right triangles \(BCK\) and \(FBK\) are similar, we may continue
\(\displaystyle \begin{align} \frac{CG}{DG} &= \frac{CK}{FK} \\ &=\frac{CK}{BK}\times\frac{BK}{FK} \\ &= \mbox{tan}\angle CBK\space\times\space\mbox{tan}\angle BFK \\ &= (\mbox{tan}\angle BFC)^{2}. \end{align} \)
For the perpendicular from \(A\), assume it intersects \(DF\) in \(J\) and \(CD\) in \(G'\). Then, similarly to the above,
\(\displaystyle \begin{align} \frac{CG'}{DG'} &= \frac{FJ}{DJ} \\ &=\frac{FJ}{AJ}\times\frac{AJ}{DJ} \\ &= \mbox{tan}\angle FAJ\space\times\space\mbox{tan}\angle ADJ \\ &= (\mbox{tan}\angle ADF)^{2}. \end{align} \)
But, since angles \(BFC\) and \(AFD\) are complementary, \(\angle BFC=\angle ADF\) and, therefore, \(\displaystyle\frac{CG}{DG}=\frac{CG'}{DG'}\) such that \(G=G'\), and we are done.
This configuration has additional properties. For examples, \(\angle AGB\) is right and \(HG\perp CD\) so that quadrilaterals \(BCGH\) and \(ADGH\) are both cyclic.
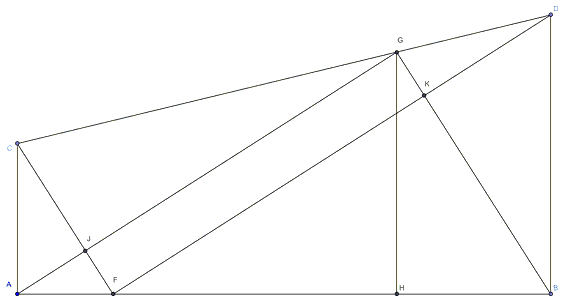
Finally, circle \(C(M)\) place an ancilary role, producing point \(F\) on \(AB\) such that \(\angle CFD=90^{\circ}\). Thus given such point a priori, we could procede with the construction as shown below:
|Contact| |Front page| |Content| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
73518034
