Dao's Variant of Thebault's First Problem
What Might This Be About?
Problem
Similarly oriented squares are constructed on the sides of a parallelogram. The sides of the parallelogram are extended to intersect the lines joining the centers of the squares, as shown:
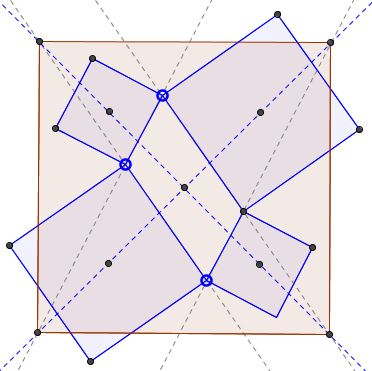
Prove that the points of the intersection form a square.
Proof 1
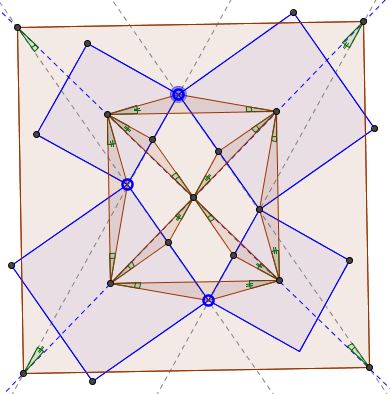
This problem is obviously related to Thébault's Problem 1. The vertices of Thébault's square lie on the lines of the centers of the constructed squares and so do the vertices of the alleged square in the present problem. Because of this and due to the central symmetry inherent in the problem, the shape in question is a rhombus. It then suffices to show that its diagonals are equal. The following diagram sheds extra light on the configuration by emphasizing two groups of equal angles. The proof that this is indeed so is left as an exercise.
The proof itself is illustrated by the diagram below. Trigonometry is the main tool, especially the Law of Sines.
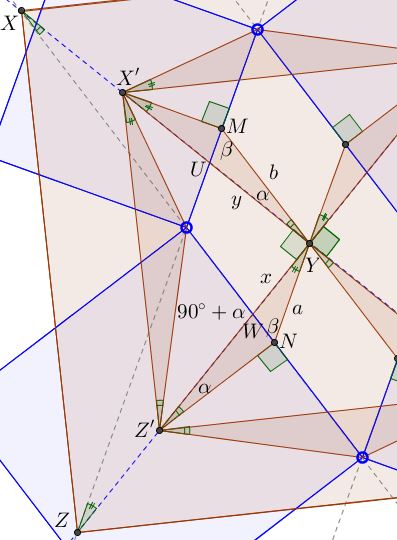
Thus we have that
(1)
$X'Y=YZ'$
and have to show that
(2)
$XY=YZ.$
In $\Delta NYW,$ $\displaystyle x=\frac{a\sin\beta}{\cos\alpha}.$ In $\Delta XYW,$ $XY=x\tan (90^{\circ}-\alpha )$ such that
$XY=\displaystyle\frac{a\sin\beta}{\cos\alpha}\cdot\frac{\cos\alpha}{\sin\alpha}=\frac{a\sin\beta}{\sin\alpha}.$
In $\Delta MUY,$ $y=\displaystyle\frac{b\sin\beta}{\sin (\alpha+\beta )}.$ In $\Delta UYZ,$ $YZ=y\tan (\alpha +\beta ),$ i.e.,
$YZ=\displaystyle\frac{b\sin\beta}{\sin (\alpha+\beta )}\cdot\frac{\sin (\alpha+\beta )}{\cos (\alpha+\beta )}=\frac{b\sin\beta}{\cos (\alpha+\beta)}.$
In $\Delta MX'Y,$ $X'Y=\displaystyle\frac{b\cos\beta}{\cos (\alpha+\beta )},\;$ whereas in $\Delta NYZ',$ $YZ'=\displaystyle\frac{a\cos\beta}{\sin\alpha}.$ Since $X'Y=YZ',$ we find the relation between $a\;$ and $b:$
$\displaystyle\frac{b\cos\beta}{\cos (\alpha+\beta )}=\frac{a\cos\beta}{\sin\alpha},$ or $b=\displaystyle\frac{a\cos(\alpha+\beta) }{\sin\alpha}.$
It follows that
$\displaystyle YZ=b\frac{\sin\beta}{\cos (\alpha+\beta)}=\frac{a\cos(\alpha+\beta) }{\sin\alpha}\cdot\frac{\sin\beta}{\cos (\alpha+\beta)}=\frac{a\sin\beta}{\sin\alpha}=XY,$
as required.
Proof 2
This proof is by Grégoire Nicollier and is one of the series of spectral proofs. It is directly based on his solution to Thébault's first problem which we reproduce first.
Let $q=(1,\,i,\,-1,\,-i)$ be the positively oriented unit square of the complex plane. Any nontrivial parallelogram $Q$ centered at the origin of the complex plane can be expressed up to a spiral similarity as $Q=q+b\bar q$ for some $b=x+iy\;$ or $Q=\bar q$. We suppose $Q=q+b\bar q$. Let $T(Q)$ be the quadrilateral obtained by erecting isosceles right-angled right-hand ears on the sides of $Q$. The transformation $T$ is linear and deletes $\bar q$: thus $T(Q)=T(q+b\bar q)=T(q)=\sqrt2e^{i\pi/4}q\;$ is a square.
Now, for Dao's extension.
An easy computation shows that the line through the vertices $i-ib$ and $1+b$ of $Q$ and the diagonal $t(1-i)$ of $T(Q)$ concur for $t=\left(x^2+ y^2-1\right)/(2x)$, as do the line through the vertices $-i+ib$ and $1+b$ of $Q$ and the diagonal $t(1+i)$ of $T(Q)$.
Acknowledgment
The problem has been posted by Dao Thanh Oai at the CutTheKnotMath facebook page.
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73579172
