Excircles Variant of Thébault's Problem III
A problem by Victor Thébault that he came up with in 1938 has a long history outline elsewere
Let \(AM\) be a cevian in \(\Delta ABC\), \(M\) between \(B\) and \(C\). Construct two circles that touch \(BC\), \(AM\) and the circumcircle of \(\Delta ABC\) and denote their centers as \(P\) and \(Q\). Let \(I\) be the incenter of \(\Delta ABC\). Then \(P\), \(I\), \(Q\) are collinear.
More recently Sohail Farhangi came up with an elementary proof of Y. Sawayama's Lemma which directly leadds to a solution of Thébault's problem and, in addition, observed that his proof adapts to the case where the two circles touch the triangles and its circumcircle externally. Sohail put his results in a pdf file, while below I shall present what he calls the "external case".
Theorem
Given triangle \(ABC\), construct its circumcircle \(T\). Now take any point \(D\) on side \(BC\) and draw line \(AD\). Now construct the \(2\) circles \(C(O_1)\) and \(C(O_2)\) that are externally tangent to \(T\), \(BC\), and \(AD\), with centers \(O_1\) and \(O_2\) respectively. Let \(I_A\) be the excenter of \(\Delta ABC\) with respect to \(A\). \(O_1\), \(O_2\), and \(I_A\) are collinear.
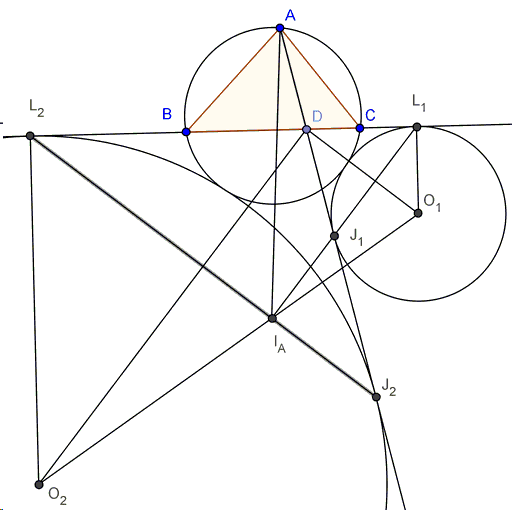
The proof is based on the following
Lemma
Under the conditions of the theorem, let \(C(O_1)\) be tangent to \(T\) at \(K\), \(BC\) at \(L\), and \(AD\) at \(J\). \(I_A\), \(L\), and \(J\) are collinear.
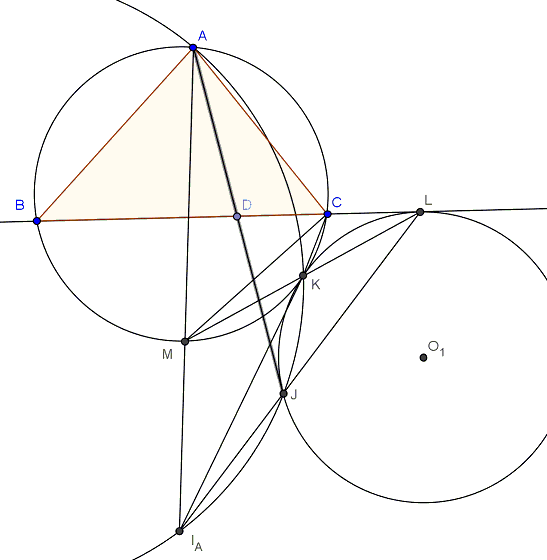
Proof of Lemma
Let \(LI_A\) intersect \(C(O_1)\) at \(J'\). We will show that \(J'\) and \(J\) coincide. Let \(KL\) intersect \(T\) for a second time at \(M\). We can see from homothety that \(M\) is the midpoint of arc \(BC\) in \(T\). Similarly, from homothety we can see that \(KL\) and \(KM\) subtend arcs of equal angles in \(C(O_1)\) and \(T\) respectively. We now have \(\angle LJ'K = \angle MAK = \angle I_AAK = 180^{\circ}-\angle KJ'I_A\), which tells us that \(A\), \(I_A\), \(J'\), \(K\) are concyclic. Now observe that \(\angle MCL = 180^{\circ}-\angle MCB = 180^{\circ}-\angle MBC = \angle MKC\), implying similarity of triangles\(MLC\) and \(MCK\), from which \((MC)^2 = ML\times MK\). Noting the well known fact that \(MI_A = MC\), we have \((MI_A)^2 = ML\times MK\) so that triangles \(MI_AL\) and \(MKI_A\) are similar and, therefore, \(\angle MI_AK = \angle MLI_A\), and \(\angle KLI_A = \angle KI_AA = \angle KJ'A\), which tells us that \(AJ'\) is tangent to \(C(O_1)\) as desired.
Proof of Theorem
Let \(C(O_i)\) be tangent to \(AD\) and \(BC\) at \(J_i\) and \(L_i\) respectively for \(i = 1, 2\).

Note that \(\angle O_1DO_2 = 90^{\circ}\) as \(O_1D\) and \(O_2D\) are the internal and external angle bisectors of \(\triangle BDJ_1\) respectively. We also know that \(O_iD \perp J_iL_i\) for \(i = 1, 2\), which lets us identify right trapezoid \((O_1L_1L_2O_2)\), and exploit a property proved elsewhere, thus establishing the collinearity of \(O_1\), \(O_2\), and \(I_A\).
|Contact| |Front page| |Contents| |Geometry| |Eye opener|
Copyright © 1996-2018 Alexander Bogomolny
73576819
