A New Geometrical Proposition

By Y. SAWAYAMA, Instructor in The Central Military School for Boys, Tokyo, Japan.

General enunciation. Describe eight circles, each of which touches a circle and any two secants of it; next construct a triangle by joining any three of the points of intersection of the latter circle and the two secants; then the chords of contact and the line of centers of two of the eight circles taken appropriately in pairs are concurrent, the point of concurrency being equidistant from the three sides of the triangle.

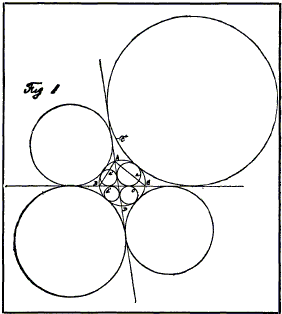
Particular enunciation. Call the circle, ABC, the eight circles a, a', b, b', c, c', d, d', and the two secants AD, BC (Fig. 1). Then

1. The line of centers of the two circles a and a', and their two chords of contact pass through the center of the inscribed circle of the triangle ABC.
2. The line of centers of the two circles b and b', and their two chords of contact pass through the center of the circle escribed to the side BC of the triangle ABC.
3. The line of centers of the two circles c and c', and their two chords of contact pass through the center of the circle escribed to the side CA of the triangle ABC.
4. The line of centers of the two circles d and d', and their two chords of contact pass through the center of the circle escribed to the side AB of the triangle ABC.

Demonstration. Let K, E, and F be the three points of contact where any one of the eight circles touches the circle ABC and the two secants BC, AD (Figs. 2 and 3). Then as is well known, we have two properties:

1. The line KE passes through the middle point M of the arc BC, so also the line KF through the middle point M of the arc AD.
2. The two straight lines EF and MN are parallel.

From the last property we have ∠EFK = ∠MNK, and as the four points M, N, A, and K lie on the circle ABC, ∠MNE = ∠MAE (Fig. 2), or = its supplementary angle (Fig. 3).

∴ ∠EFK = ∠MAK or = its supplementary angle. Hence the four points A, K, F, and I (which is the intersection of EF and AX) are concyclic.

∴ ∠AIK = ∠AFK (Figs. 2 and 3), or = its supplementary angle (figure omitted). Now the line AF touches the circle EFK, hence ∠AFK or its supplementary angle = FEK. ∴ ∠AIK= ∠FEK.

∴ ΔMKI and ΔMIE are mutually equiangular, from which we can deduce that the circle passing through the three points I, E, and K touches the line MI, hence MI² = MK×ME. On the other hand, since arc MB = arc MC, we have ∠MKB = ∠MBE (in the figures we omit the line BK).

∴The circle passing through the three points B, E, and K touches the line MB, hence we have MK×ME = MB², or MI² = MB², MI = MB.

This shows that I is equidistant from the three sides of the triangle ABC.

Next, call 0 the center of the circle EFK, L the intersection of BC and AD, P the intersection of EF and OL, Q another intersection of 0I and the circle BIC, and draw the straight line passing through Q and L (Fig. 4).

Then the square of the tangent drawn from the center of the circle BIC to the circle EFK is equal to the rectangle MK×ME, or the square of the radius of the circle BIC.

This last fact shows that the two circles EFK and BIC are orthogonal, and the radius OE of the circle EFK is equal to the tangent drawn from the point 0 to the circle BIC, and that 0E² = OQ×OI.

Again, in the right-angled triangle OLE, 0E² = OL×OP. ∴ OQ×OI = OL×OP.

∴ The four points I, P, L, and Q are concyclic.

Noting the angle IPL is a right angle and the ∠IQL and ∠IPL are equal or supplementary, we have ∠IQL = 90°.

∴ The line QL passes through a point I' which is equidistant from the three sides of the triangle ABC (I' is, in fact, the other extremity of the diameter passing through I of the circle BIC). And the line 0I is perpendicular to a fixed line I'L passing through the fixed point Q on it.

Similarly, the center of another circle whose chord of contact passes through the point I, and the point I are on the straight line which is perpendicular to I'L and passes through the fixed point Q on it. Therefore the centers of the two circles whose chords of contact pass through I and the point I are collinear.

Corollary I. In the preceding figures, the point of intersection (other than I) of the circle BIC and the line EF is one of the points which are equidistant from the three sides of the triangle DBC.

One of the two intersections of the line EF and the circle whose center is N and whose radius is NA is equidistant from the three sides of the triangle BAD, and the other from the three sides of the triangle CAD.

Corollary II. In Fig. 1 the points of contact of the eight circles with either of the two secants are in involution, the center of which is the intersection L of the two secants, and then its constant is equal to the power of the point L with respect to the circle ABC.

Demonstration. Take L, the intersection of two secants AD and BC as the center of inversion, and the power of L with respect to the circle ABC for the constant of inversion. In the figures 3, and 3, call E', F', and K', the inverses of the three points E, F, and K, respectively. Then as the two secants EC and AD, and the circle ABC are their own inverses, the circle E'F'K' which is the inverse of the circle EFK, touches the secants BC and AD and the circle ABC.

Corollary III. When AD and BC are perpendicular, the centers of the four circles a, b, a', b' are concyclic; so also those of a, b, c, d; those of a', b', c', d', and those of c, d, c', d'.

References

1. Y. Sawayama, A New Geometrical Proposition, The American Mathematical Monthly, Vol. 12, No. 12. (Dec., 1905), pp. 222-224.

Related material Read more...
	Thébault's Problems
	Thébault's Problem I
	Thébault's Problem II
	Thébault's Problem III
	Y. Sawayama's Lemma
	Jack D'Aurizio Proof of Sawayama's Lemma
	Thébault's Problem III, Proof (J.-L. Ayme)
	Circles Tangent to Circumcircle
	Thébault's Problem IV
	A Property of Right Trapezoids
	A Lemma on the Road to Sawayama
	Excircles Variant of Thébault's Problem III
	In the Spirit of Thebault I
	Dao's Variant of Thebault's First Problem

|Contact| |Front page| |Contents| |Geometry| |Eye opener|

Copyright © 1996-2018 Alexander Bogomolny