Thébault's Problem III, Proof
The applet illustrates a synthetic solution for Thébault's Problem III. See if you can surmise what is it about before proceeding to the explanation.
|Activities| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
The applet illustrates a solution to Thébault's Problem III by Jean-Louis Ayme (2003).
By the construction, PG and QE are both perpendicular to BC; so PG||QC. By Sawayama's Lemma, both EF and GH pass through the incenter I of ΔABC. Triangles DHG and QGH being isosceles in D and Q, DQ is
- the perpendicular bisector of GH,
- the D-internal bisector of ΔDHG.
Mutatis mutandi, DP is
- the perpendicular bisector of EF,
- the D-internal bisector of ΔDEF.
As the bisectors of two adjacent and supplementary angles are perpendicular,
Michel Cabart found an alternative ending:
D is barycenter of E and G, with coefficients DG and DE, thus
| (1) | ID = (DG/GE)·IE + (DE/GE)·IG |
Let α be the angle of DP with respect to DE
IE = GE·sinα thus IE = (GE sinα)·(QD/QD)
IG = GE·cosα thus IG = (GE cosα)·(PD/PD)
Replacing in (1) yields
| ID | = (DG sinα/QD)·QD + (DE cosα/PD)·PD | |
| = (sin²α)·QD + (cos²α)·PD. |
thus I is barycenter of Q and P with coefficients sin²α and cos²α and, as such, is collinear with both.
A third prove has been discovered by Sohail Farhangi; it is based on a property of right trapezoids proved elsewhere. The right trapezoid to consider is EPQG
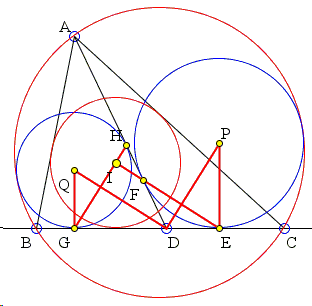
For any choice of D, DP⊥DQ because they are bisectors of supplementary angles. Then the property of right trapezoids forces IG and IE to be perpendicular, with I lying on PQ.
References
|Activities| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
73579093
