Jack D'Aurizio Proof of Sawayama's Lemma

Through vertex A of ΔABC a straight line AD is drawn with D on BC. Let circle C1 tangent to AD at F, CD at E, and the circumcircle C2 of ΔABC at K. Then the chord EF passes through the incenter I of ΔABC.

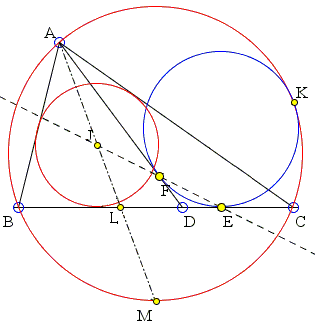
a proof of Sawayama's theorem

Proof

By Casey's theorem, applied to A, B, C (as 1-point circles) and circle C1 (all "touching" C2), we have that:

AF · BC + AB · CE = AC · BE

that is equivalent to:

(1) a · AF + a·c = (b + c) BE,

where a, b, c are the lengths of sides BC, AC, and AB, as usual.

Let L be the inetersection of BC with the bisector AI of angle at A. Consider now the six points A, I, L, D, E, F. In virtue of Menelaus' theorem and its converse, E, F, I are collinear if and only if in ΔADL,

(LE/DE) · (DF/AF) · (AI/IL) = 1

Which is equivalent to:

(LE/AF) · (AI/IL) = 1

because DE = DF. In virtue of the angle bisector theorem and the Van Obel theorem we have that:

AI/IL = (b + c)/a,

so, in order to prove the collinearity of I, E, F, suffice it to prove that:

(2) a · AF = LE · (b + c).

Again by the angle bisector theorem, BL = ac / (b + c). Now, LE = BE - BL = BE - ac/(b + c), so that (1) implies (2) and we are done.

Note: There is another poof due to Sohail Farhangi.

Related material
Read more...

Thébault's Problems

  • Thébault's Problem I
  • Thébault's Problem II
  • Thébault's Problem III
  • Y. Sawayama's Lemma
  • Y. Sawayama's Theorem
  • Thébault's Problem III, Proof (J.-L. Ayme)
  • Circles Tangent to Circumcircle
  • Thébault's Problem IV
  • A Property of Right Trapezoids
  • A Lemma on the Road to Sawayama
  • Excircles Variant of Thébault's Problem III
  • In the Spirit of Thebault I
  • Dao's Variant of Thebault's First Problem

    • |Contact| |Front page| |Contents| |Geometry| |Eye opener|

    Copyright © 1996-2018 Alexander Bogomolny

    71876427