|
|
|
|
|
|
|
|
|
Reflections of the Orthocenter: What Is It About?
|
| Buy this applet What if applet does not run? |
Copyright © 1996-2008 Alexander Bogomolny
Reflections of the Orthocenter
The applet suggests the following theorem [F. G.-M., p. 142; Honsberger, pp. 17-18; Lalesco, 1.11] from triangle geometry:
| The reflections of the orthocenter of a triangle in the side lines of the latter lie on its circumcircle. |
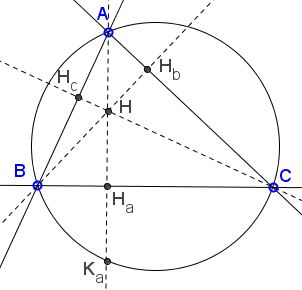
Let H be the orthocenter of 
ABC with an altitude AHa. Denote the second point of intersection of AHa with the circumcircle as Ka. We wish to prove that
| (1) | HHa = HaKa. |
In the following I assume that ABC is acute. If one of its angles is obtuse, the derivation is just a little different.
| Buy this applet What if applet does not run? |
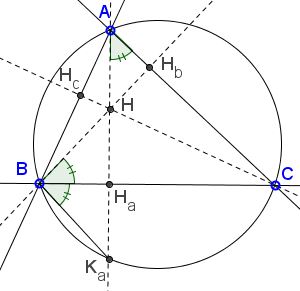
Let BHb be another altitude of ABC. Since the right triangles CAHa and CBHb share angle C, their other acute angles (CAHa and CBHb) are equal:
| (2) |
 CAHa = CBHb.
|
On the other hand, the inscribed angles CAKa and CBKa are subtended by the same arc CKa. Therefore,
| (3) |
CAHa = CBKa.
|
From (2) and (3),
| (4) |
CBHb = CBKa.
|
Thus BHa is simultaneously an altitude and an angle bisector in BHKa. It's then also a median from B to HKa, which immediately implies (1).
The circumcevian triangle of the orthocenter is known as the circum-orthic triangle.
For the sake of future references, let's observe that the points A, B, C, and Ka, Kb, and Kc divide the circumcircle into 3 pairs of arcs, the two arcs in a pair around any of the vertices A, B, or C being equal. The angular measure of the arcs next to A is twice BAC
The circle through H, B, and C is the reflection of the circumcircle in BC and thus has the same radius. In addition, the reflection S of the vertex A lies on that circle: ABC could be treated similarly, which leads to the following result:
| The circumcircles of triangles ABC, ABH, BCH, and CAH are all equal. |
The circumcircles of triangles AKbKc, BKcKa, CKaKb naturally coincide with the circumcircle of ABC. In a more general case where points Ka, Kb, Kc are the reflections of an arbitrary point in the side lines of ABC, the circumcircles of triangles AKbKc, BKcKa, CKaKb are concurrent and meet on the circumcircle of ABC.
References
- F. G.-M., Exercices de Géométrie, Éditions Jacques Gabay, sixiéme édition, 1991
- R. Honsberger, Episodes in Nineteenth and Twentieth Century Euclidean Geometry, MAA, 1995.
- T. Lalesco, La Géométrie du Triangle, Éditions Jacques Gabay, sixiéme édition, 1987
Copyright © 1996-2008 Alexander Bogomolny
| 29537424 |  |
|