A Proof of the Pythagorean Theorem with Orthocenter and Right Isosceles Triangles

Quang Tuan Bui

ABC is a triangle right at C with sides a, b, c and circumcircle (O) centered at O, the midpoint of the hypotenuse AB. Suppose b ≤ a.

Construct point M on the ray BC such that CM = AC = b and M is outside segment BC. The line AM intersects circle (O) again at D. Since b ≤ a D is on the semicircle other than the semicircle which contains C.

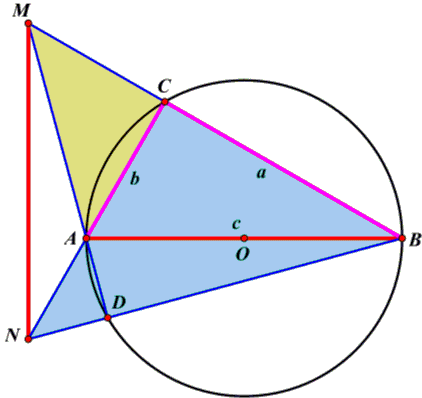
The intersection N of AC and BD is on the ray BD and is outside the segment BD. Therefore:

Area(ΔBMN) = Area(ΔMNA) + Area(ΔCNB) + Area(ΔCMA)
Area(ΔBMN) - Area(ΔMNA) = Area(ΔCNB) + Area(ΔCMA)

It follows that A is the orthocenter of ΔBMN, implying

ΔMCA is right isosceles suh that triangles NDA, NCB, MDB are also right isosceles.

Two right triangles CMN and CAB are congruent (because CM = CA, CN = CB) therefore MN = AB = c and from (1) we have:

c²/2 = Area(ΔCNB) + Area(ΔCMA)
c²/2 = a²/2 + b²/2
c² = a² + b².

which is the Pythagorean identity.

The Orthocenter

1. Count the Orthocenters
2. Distance between the Orthocenter and Circumcenter
3. Circles through the Orthocenter
4. Reflections of the Orthocenter
5. CTK Wiki Math - Geometry - Reflections of the Orthocenter
6. Orthocenter and Three Equal Circles
7. A Proof of the Pythagorean theorem with Orthocenter and Right Isosceles Triangles
8. Reflections of a Line Through the Orthocenter
9. Equal Circles, Medial Triangle and Orthocenter
10. All About Altitudes
11. Orthocenters of Two Triangles Sharing Circumcenter and Base
12. Construction of a Triangle from Circumcenter, Orthocenter and Incenter
13. Reflections of the Orthocenter II
14. Circles On Cevians

|Contact| |Front page| |Contents| |Geometry| |Pythagorean theorem| |Store|