Determinants, Area, and Barycentric Coordinates

Let the vertices of ΔABC have coordinates A(x_A, y_A), B(x_B, y_B), and C(x_C, y_C). Define two planar vectors (x_B - x_A, y_B - y_A) and (x_C - x_A, y_C - y_A). From the expression for their vector product we arrive at a formula for the area of ΔABC. The area is half the absolute value of the determinant

which can also be written as

(1)

Determinants are introduced in Linear Algebra and are mostly used for solving linear equations. No one likes Cramer's rule, and there are much simpler ways to solve a system of linear equations. However, there is nothing like determinants to compress long expressions into a very concise form. I'll need just the linearity property of determinants. Using boldface to denote whole columns of a determinant, linearity means that

(2)	| ka + mb c d | = k | a c d | + m | b c d |

A determinant with two equal columns is zero which is only a very particular case of a much more general statement. Returning to the triangle ABC, let there be three points K₁, K₂, and K₃ in the interior of ΔABC. I want to express the area of ΔK₁K₂K₃ in terms of area(ΔABC).

Let the barycentric coordinates of the three points (u₁, v₁, w₁), (u₂, v₂, w₂), and (u₃, v₃, w₃) normalized so that, for i = 1, 2, 3,

(*)	ui + vi + wi = 1.

Then, for i = 1, 2, 3, we have

K_i = (u_ix_A + v_ix_B + w_ix_C, u_iy_A + v_iy_B + w_iy_C)

Use now (1) to express the area of ΔK₁K₂K₃ as a determinant. Apply repeatedly the properties of determinants to obtain the following nice formula

(3)

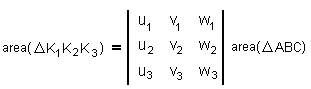
Although (3) has been derived under the condition (*), the determinant in (3) is zero or not for all equivalent representations of the three points in the barycentric coordinates. The area of the triangle K₁K₂K₃ is 0 iff the three points are collinear, i.e., all lie on the same straight line. For a generic point K(u, v, w) that lies on the line through K₁ and K₂ we have

(4)

which is an equation of a straight line through two points in barycentric coordinates, that need not satisfy (*). Thus a straight line in the barycentric coordinates is given by a linear homogeneous equation uU + vV + wW = 0 for some coefficients U, V, and W not all of which are 0.

With the tools we now possess we can solve an interesting problem:

Given a point K inside a ΔABC, let E, D, F be the feet of the cevains through K on BC, AC, AB. Determine K such that the area of triangle DEF is as large as possible. (Solution)

Note that (4) supplies an algebraic proof of Menelaus' theorem. Indeed, assume there are three points A', B', C' on the sides of triangle ABC. In the barycentric coordinates the points can be written as

(5)	A' = (0, v1, w1), B' = (u2, 0, w2), and C' = (u3, v3, 0).

The corresponding determinant evaluates to

u3· v1· w2 + u2· v3· w1.

The three points are collinear iff the determinant is 0, which is equivalent to

u3/u2· v1/v3· w2/w1 = -1.

We can also prove a generalization of Ceva's theorem due to E. J. Routh (1896).

For simplicity, in (5), I'll use a somewhat different form of the barycentric coordinates:

(5')	A' = (0, 1, λ), B' = (μ, 0, 1), and C' = (1, ν, 0).

This is always possible. Note that the points A', B', C' are located on the side lines BC, AC and AB, respectively. In general, the three lines AA', BB' and CC' form a triangle whose area is established by Routh's theorem. The area of that triangle vanishes iff the three lines are concurrent which, as we shall see shortly, leads to Ceva's theorem.

In the barycentric coordinates (u, v, w) the lines AA', BB' and CC' have equations (see (4)):

AA': λv = w,
BB': μw = u
CC': νu = v.

Further, the lines AA' and BB' intersect in point (λμ, 1, λ) and similarly for the other two pairs of the lines. We may use (3) to determine the area of the triangle defined by the three lines relative to that of ΔABC. The determinant in (3) evaluates to (λμν - 1)², which, according to (*), must be divided by (μ + μν + 1)(1 + ν + λν)(λμ + 1 + λ), which results in Routh's theorem:

Theorem

If three points A'(0, 1, λ), B'(μ, 0, 1), C'(1, ν, 0) are selected on the sides BC, AC, and AB of triangle ABC of unit area. Then the area of the triangle formed by the three lines AA', BB', CC' is given by

(6)	(λμν - 1)2 / (μ + μν + 1)(1 + ν + λν)(λμ + 1 + λ).

Ceva's theorem is an immediate consequence of (6).

Formula (6) helps us verify a more specialized result where λ = μ = ν. In particular, whenever each of these equals 2, (6) implies that the area of the small triangle equals (2³ - 1)² / (4 + 2 + 1)³ = 1/7. (There is a nice proof without words for the latter result and its generalization.)

In passing, the area of triangle A'B'C' relative to that of ABC is given by

(7)	(λμν + 1) / (λ + 1)(μ + 1)(ν + 1).

The latter formula implies Menelaus' theorem.

References

1. G. Chang and Th. W. Sederberg, Over And Over Again, MAA 1997
2. H. S. M. Coxeter, Introduction to Geometry, John Wiley & Sons, 1961

Barycenter and Barycentric Coordinates

1. 3D Quadrilateral - a Coffin Problem
2. Barycentric Coordinates
3. Barycentric Coordinates: a Tool
4. Barycentric Coordinates and Geometric Probability
   • Stick Broken Into Three Pieces (Trilinear Coordinates)
   • Stick Broken Into Three Pieces (Cartesian Coordinates)
5. Ceva's Theorem
6. Determinants, Area, and Barycentric Coordinates
7. Maxwell Theorem via the Center of Gravity
8. Bimedians in a Quadrilateral
9. Simultaneous Generalization of the Theorems of Ceva and Menelaus
   • Theorems of Ceva and Menelaus, an Illustrated Generalization
10. Three glasses puzzle
11. Van Obel Theorem and Barycentric Coordinates
12. 1961 IMO, Problem 4. An exercise in barycentric coordinates
13. Centroids in Polygon
14. Center of Gravity and Motion of Material Points
15. Isotomic Reciprocity
16. An Affine Property of Barycenter
17. Problem in Direct Similarity
18. Circles in Barycentric Coordinates
19. Barycenter of Cevian Triangle
20. Concurrent Chords in a Circle, Equally Inclined

|Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny

Solution

From the definition, points D, E, and F have the following barycentric coordinates:

D(0, r_a/(r_a+1), 1/(r_a+1)),
E(1/(r_b+1), 0, r_b/(r_b+1)), and
F(r_c/(r_c+1), 1/(r_c+1), 0).

The determinant in (3) appears as

(11)

which we should maximize subject to r_ar_br_c=1. This is the same as minimizing f = (r_a + 1)(r_b + 1)(r_c + 1) under the same constraint. By direct manipulation, f = (r_a+1/r_a) + (r_b + 1/r_b) + (r_c+1/r_c) + 2. Applying Arithmetic-Geometric Mean Inequality to every term in parentheses gives f ≥ 8 with the equality attained only when r_a= r_b= r_c= 1. The answer, therefore, is that the triangle DEF has the maximum area when K is the centroid of ΔABC.

Related material Read more...
	What Is Determinant?
	Determinant and Divisibility
	Vandermonde matrix and determinant
	Cabart's Collinearity
	Three Similar Triangles
	Vandermonde Determinant
	Divisibility Of Prod-Dif And The Vandermonde Determinant
	Determinant on a Circle
	A Case for Determinants
	A Cyclic Inequality in Three Variables with a Variable Hierarchy

|Contact| |Front page| |Contents| |Geometry| |Up|

Copyright © 1996-2018 Alexander Bogomolny