Three Colors - Two Points

Points in the plane are each colored with one of three colors: red, green, or blue. Prove that, for a given distance d, there are always two points of the same color at the distance d from each other.

Solution

Solution 1

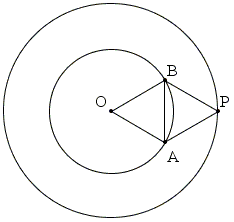
two equilateral triangles back-to-back

Pick any point O. Let it be red. Draw a circle of radius √3d. There are two possibilities. All points on that circle are red or there is a point that is either green or blue. In the first case, the endpoints of any chord of length d will be of the same color (red), thus solving the problem. Otherwise, let there be green point P. Find two points A and B that form two equilateral triangles OAB and PAB of side d. The points are the intersections of the two circle O(d) and P(d), centered at O and P and both with radius d.

One of A and B may be either red or green. Together with O or P we would have a monochromatic pair. Otherwise, they both are blue and at distance d and so form a monochromatic pair.

Solution 2

A. Soifer credits Leo and William Moser with that solution but the proper reference is missing from the book. Soifer dates the solution at 1961.

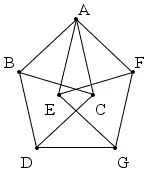
Leo and William Moser's Spindle

In the figure which is now known as Moser's Spindle, the distances AB, AC, AE, AF, BC, BD, EF, FG, DG, EG, CD are all d. Let A be red. If either B or C are of the same color or one of them is red we are done. So assume B is green and C is blue. If D is either green or blue, we are done. So assume D is red.

Similarly, checking the colors of E and F, unless there is a monochromatic pair, we arrive at a red G. But then D and G form a monochromatic pair.

Reference

A. Soifer, Geometric Etudes in Combinatorial Mathematics, Springer, 2010 (2nd, expanded edition), pp. 237

71868275