Tiling Square with Tetrominoes Fault-Free

There are five types of tetromino (a polyomino that consist of four squares):

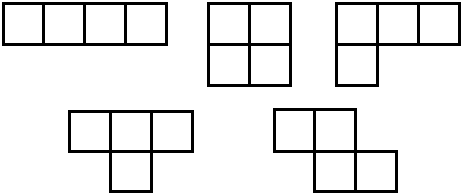
all five types of tetromino

These are called "straight", "square", "L-tetromino", "T-tetromino", and "skew" or "Z-tetromino".

Four types of tetromino (all, except the skew) tile an 8×8 chessboard. In fact, each of these already tiles a 4×4 square:

four tetromino types tile a 4x4 square

The covering of an 8×8 chessboard in this manner with a unique type of tetromino would introduce fault lines - the straight lines between squares that run from edge to edge.

  1. Every tiling of an 8×8 chessboard with straight tetrominoes contains a fault line.
  2. Every tiling of an 8×8 chessboard with square tetrominoes contains a fault line.
  3. An 8×8 chessboard can be tiled with no fault lines by T-tetromino.
  4. An 8×8 chessboard can be tiled with no fault lines by L-tetromino.

The first two claims are almost obvious or become so after short experimentation. The simplest way is to start from a corner tile and see how a tiling may evolve from there. (This is also a good approach to proving that the skew tromino does not tile a rectangle, let alone a square.)

There is a very general result (1981) by Ron Graham for the existence tiling rectangular boards with rectangular pieces:

A fault-free tiling of a p×q rectangle with a×b tiles exists (where we assume pq > ab and gcd(a, b) = 1) if and only if

  1. Each of a and b divides p or q;
  2. Each of p and q can be expressed as xa + yb, x > 0, y > 0, in at least two ways;
  3. For {a, b} = {1, 2}, {p, q} ≠ {6, 6}.

A solution to the third one is shown below.

George Jelliss found 12 solutions to the fourth problem.

References

  1. R. L. Graham, Fault-Free Tilings of Rectangles, In The Mathematical Gardner: A Collection in Honor of Martin Gardner (Ed. D. A. Klarner), Van Nostrand Reinhold (March 1982)

|Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny

Solutions

An 8×8 chessboard can be tiled with no fault lines by T-tetromino.

One solution is found at [Martin, p. 48]:

fault-free tiling of 8×8 square with T-trominoes

An 8×8 chessboard can be tiled with no fault lines by L-tetromino.

George Jelliss found 12 solutions. George has observed that the first three are symmetric; the second and third differ only by rotation of the central pair; I find the latter especially remarkable.

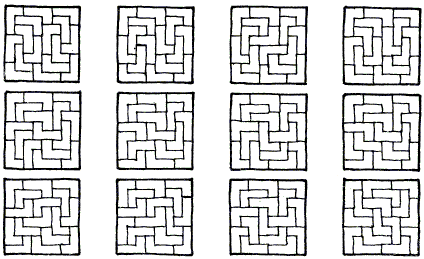
fault-free tiling of 8×8 square with L-trominoes

References

  1. G. E. Martin, POLYOMINOES: A Guide to Puzzles and Problems in Tiling, MAA, 1996

Related material
Read more...

  • Covering A Chessboard With Domino
  • Dominoes on a Chessboard
  • Tiling a Chessboard with Dominoes
  • Vertical and Horizontal Dominoes on a Chessboard
  • Straight Tromino on a Chessboard
  • Golomb's inductive proof of a tromino theorem
  • Tromino Puzzle: Interactive Illustration of Golomb's Theorem
  • Tromino as a Rep-tile
  • Tiling Rectangles with L-Trominoes
  • Squares and Straight Tetrominoes
  • Covering a Chessboard with a Hole with L-Trominoes
  • Tromino Puzzle: Deficient Squares
  • Tiling a Square with T-, L-, and a Square Tetrominoes
  • Tiling a Rectangle with L-tetrominoes
  • Tiling a 12x12 Square with Straight Trominoes
  • Bicubal Domino

    • |Contact| |Front page| |Contents| |Geometry|

    Copyright © 1996-2018 Alexander Bogomolny

    70561537