Property of Angle Bisectors
What is this about?
A Mathematical Droodle
| Buy this applet What if applet does not run? |
|Activities| |Contact| |Front page| |Contents| |Geometry| |Store|
Copyright © 1996-2015 Alexander BogomolnyAngle bisectors divide the opposite side in the ratio of the adjacent sides. More accurately,
If, in ΔABC, AD is an angle bisector of angle A, then
AB/AC = DB/DC.
Note that the same holds also for the external angle bisectors.
| Buy this applet What if applet does not run? |
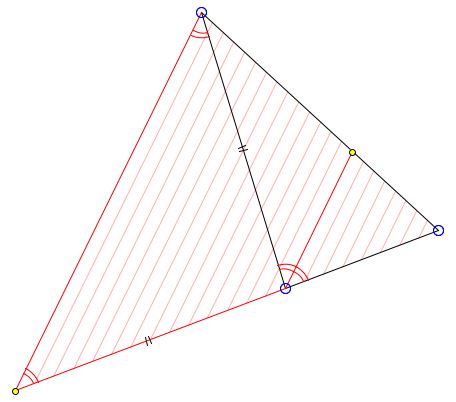
Proof
Assume the straight line through C parallel to AD meets AB in E. Then, first of all, ΔAEC is isosceles:
∠ACE = ∠CAD = ∠BAD = ∠AEC.
Therefore, AE = AC, and the required proportion follows from the similarity of triangles BEC and BAD. (There is a less standard proof.)
This property of angle bisectors is one way to show that the three angle bisectors in a triangle meet in a point. The result is an immediate consequence of Ceva's theorem.
Last note: the converse theorem holds as a matter of course, because there is only one point on a given segment that divides it in a given ratio. Thus if a point divides the base of a triangle in the ratio equal to the ratio of the sides, it is bound to be the foot of the angle bisector from the apex.
|Activities| |Contact| |Front page| |Contents| |Geometry| |Store|
Copyright © 1996-2015 Alexander Bogomolny| 49552192 |
