Condition to Have a 60 Degrees Angle
Problem
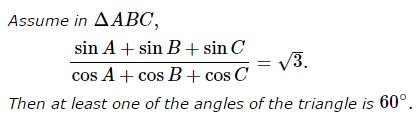
Proof
We use the following lemma which is easily proved:
If $P+Q+R=0\;$ then
$\displaystyle\sin P+\sin Q+\sin R=-4\sin\frac{P}{2}\sin\frac{Q}{2}\sin\frac{R}{2}.$
Since $\sqrt{3}=\displaystyle\frac{\sin 60^{\circ}}{\cos 60^{\circ}},$ the given relation may be written as
$\displaystyle\sum_{cyc}(\sin A\cos 60^{\circ}-\cos A\sin 60^{\circ})=\sum_{cyc}\sin (A-60^{\circ})=0.$
By Lemma, $\displaystyle\prod_{cyc}\sin\frac{A-60^{\circ}}{2}=0,\;$ and thus at least one of the factors is $0.$
Acknowledgment
This problem has been proposed by W. J. Blundon [1966, 1122, Am Math Monthly]. The solution is by A. Krishnamurthi [1968, E 1936, Am Math Monthly, p 405].
- Condition to Have a 60 Degrees Angle
- Fermat in a Triangle with a 60 Degrees Angle
- Triangle with a 60 degrees angle
- Euler Line in a Triangle with a 60 Degrees Angle
- Euler Line Cuts Off Equilateral Triangle
- 9 Point Center on Angle Bisector
- Orthic Triangle in a Triangle with a 120 degrees angle
- Klamkin's Quickie via Peru Geometrico
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73580873
