Orthic Triangle in a Triangle with a 120 degrees angle
What Might This Be About?
13 February 2017, Created with GeoGebra
Source
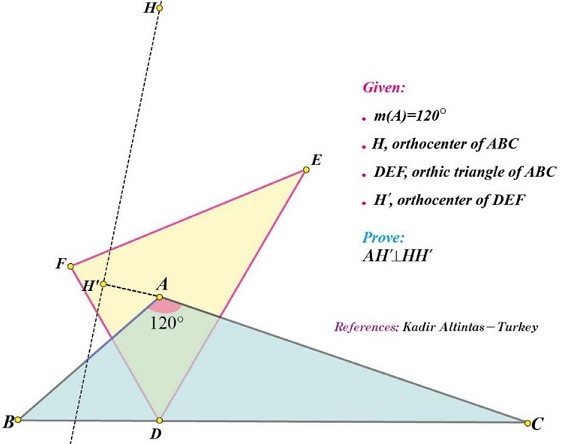
Problem
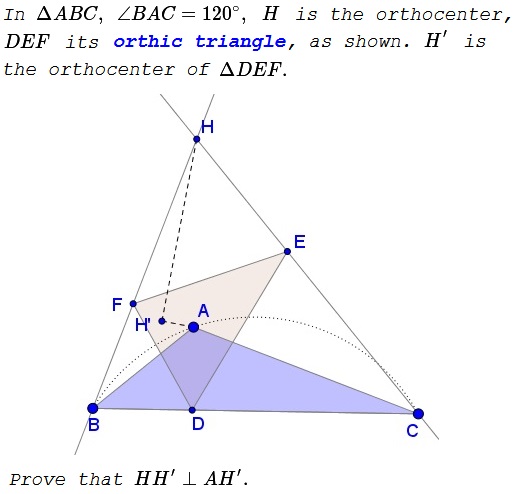
Remark
It's a well known property that three vertices of a triangle and its orthocenter form what is called the orthocentric system: the triangle formed by any three of the four points has the fourth point as its orthocenter. From this it follows that all four triangles share the same orthic triangle and, therefore, the orthocenter of the orthic triangle is one and the same for all four. If we consider just two pairs of triangle/orthocenter, e.g., $\{\Delta ABC, H\}\,$ and $\{\Delta HBC, A\},\,$ then, $A\,$ and $H\,$ simply swap their roles but not their locations, so the relation $HH'\perp AH',\,$ if it holds for one pair, necessarily holds for the other also.
Further, simple angle chasing shows that if $\angle BAC=120^{\circ},\,$ then $\angle BHC=60^{\circ}.\,$ This informs us that if the statement above holds for a triangle with a $120^{\circ}\,$ angle it also holds for triangles with a $60^{\circ},\,$ and vice versa.
Proof
With $\angle BAC =120^{\circ},$ it follows (since the quadrilateral $AEHF\,$ is cyclic) that $\angle BHC=60^{\circ},\,$ implying HCA=30^{\circ}\,$ and $\angle HDE=30^{\circ}\,(1).$
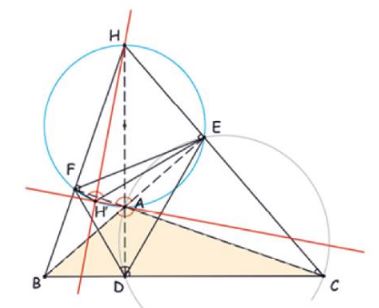
The The altitude in $\Delta ABC\,$ are the angle bisectors of the orthic triangle such that, from (1), $\angle FDE=60^{\circ}\,$ and $\angle FHE=120^{\circ}=\angle BAC=\angle FAE,\,$ making $F,H',A,E\,$ concyclic. In other words, $H'\in (AEF).$
But $\angle AFH=\angle AEH=90^{\circ},\,$ from which circle $(AEF)\,$ has $AH\,$ as a diameter. Hence $\angle AH'H=90^{\circ },\,$ i.e., $HH'\perp AH'.$
Converse
Assume in $\Delta ABC,\,$ $H\,$ is the orthocenter, $\Delta DEF\,$ the orthic triangle. Let $H'\,$ be the orthocenter of $\Delta DEF.\,$ If $HH'\perp AH',\,$ then either $\angle BAC=60^{\circ}\,$ or $\angle BAC=120^{\circ}.\,$
Because of the earlier remark we may focus on acute triangles. The diagram below illustrates angle distribution in a triangle with angles $\alpha,\,$ $\beta,\,$ $\gamma.$
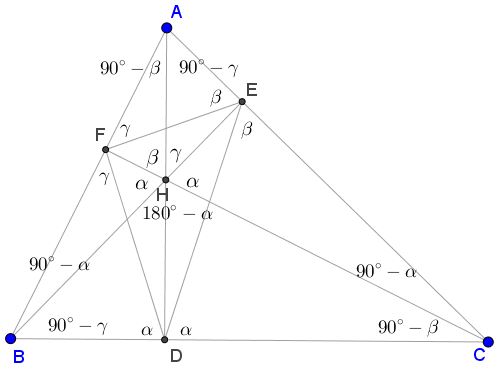
The orthic triangle comes out to have angles $180^{\circ}-2\alpha,\,$ $180^{\circ}-2\beta,\,$ $180^{\circ}-2\gamma.\,$ By analogy with, say, $\angle BHC\,$ which is supplementary to the vertex angle at $A,\,$ $\angle EH'F\,$ is supplementary to $\angle EDF=180^{\circ}-2\alpha,\,$ i.e., $\angle EH'F=2\alpha.$ Condition $HH'\perp AH'\,$ implies $H'\in (AEFH)\,$ and, subsequently, $\angle EHF=\angle EH'F,\,$ wherefrom $2\alpha=\gamma+\beta=180^{\circ}-\alpha.\,$ Thus, $\alpha=60^{\circ}.$
Acknowledgment
The above problem by Hadir Altintas (Turkey) has been posted at the CutTheKnotMath facebook page by Leo Giugiuc (Romania), with Takis Chronopoulos' English translation from the Greek of the solution by Stathis Koutras (Greece).
- Condition to Have a 60 Degrees Angle
- Fermat in a Triangle with a 60 Degrees Angle
- Triangle with a 60 degrees angle
- Euler Line in a Triangle with a 60 Degrees Angle
- Euler Line Cuts Off Equilateral Triangle
- 9 Point Center on Angle Bisector
- Orthic Triangle in a Triangle with a 120 degrees angle
- Klamkin's Quickie via Peru Geometrico
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73582836
