Euler Line in a Triangle with a 60 Degrees Angle
What Is This About?
Source
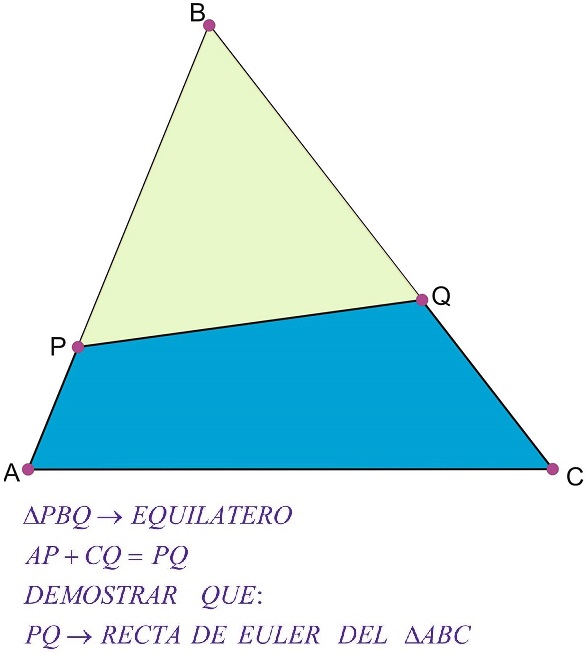
Problem
In $\Delta ABC,\;$ $\angle ABC=60^{\circ};\;$ $P\in AB,\;$ $Q\in BC\;$ such that $AP+CQ=PQ\;$ and $\Delta PBQ\;$ equilateral.
Prove that $PQ$ is the Euler line of $\Delta ABC.$
Solution 1
WLOG, choose $B=(0,\sqrt{3}),\;$ $P=(-1,0),\;$ $Q=(1,0).\;$ Let $A=(x,y).\;$ We have: $\overrightarrow{PA}=k\overrightarrow{BP},\;$ $k\gt 0,\;$ implying
$(x+1)\overrightarrow{i}+y\overrightarrow{j}=-k\overrightarrow{i}-k\sqrt{3}\overrightarrow{j}.$
From here, $A=(-(1+k),-k\sqrt{3}).\;$ Similarly, $C=(1+m,-m\sqrt{3},\;$ with $m\gt 0.\;$ From $AP+CQ=PQ\;$ we obtain $k+m=1,\;$ and from here, $-k\sqrt{3}-m\sqrt{3}+\sqrt{3}=0.\;$ This means that centroid $G\;$ of $\Delta ABC\;$ is $G=\displaystyle\left(\frac{m-k}{3},0\right),\;$ and, thus $G\in PQ.$
Let $H=(\alpha,0)\in PQ\;$ such that $BH\perp AC.\;$ This gives $\overrightarrow{BH}=\alpha\overrightarrow{i}-\sqrt{3}\overrightarrow{j}\;$ and $\overrightarrow{AC}=3\overrightarrow{i}-(k-m)\sqrt{3}\overrightarrow{j}.\;$ But $\overrightarrow{BH}\cdot\overrightarrow{AC}=0,\;$ so that $3\alpha-3(k-m)=0.\;$ In other words, $H=(k-m,0),\;$ implying that the slope of $AH\;$ is
$\displaystyle\frac{k\sqrt{3}}{2k+1-m}=\frac{k\sqrt{3}}{3k}=\frac{1}{\sqrt{1}}.$
But the slope of $BC\;$ is $-\sqrt{3},\;$ hence $AH\perp BC,\;$ making $H\;$ the orthocenter of $\Delta ABC.\;$ Since $H\in PQ,\;$ this completes the proof.
Solution 2
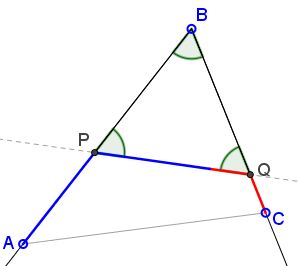
Since $AP+CQ=PQ,\;$ there is point $H\in PQ\;$ such that $AP=HP\;$ and $CQ=HQ.\;$
Triangles $APH\;$ and $CQH\;$ are isosceles with the apex angle $120^{\circ}\;$ and base angles of $30^{\circ}.\;$ Since $\angle HAP+\angle ABC=30^{\circ}+60^{\circ}=90^{\circ},\;$ $AH\perp BC.\;$ Similarly, $CH\perp AB,\;$ making $H\;$ the orthocenter of $\Delta ABC.\;$ Note that $H\in PQ.$
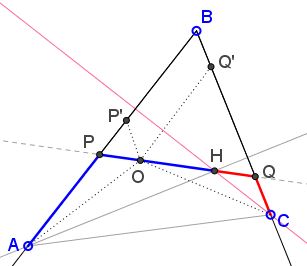
Since $AP+CQ=PQ,\;$ there is point $O\in PQ\;$ such that $AP=OQ\;$ and $CQ=OP.\;$ Triangles $APO\;$ and $CQO\;$ are equal, making $\Delta AOC\;$ isosceles. Thus, $O\;$ lies on the perpendicular bisector of $AC.\;$ We'll show that it also lies on the perpendicular bisectors of $AB\;$ and $BC.$
For example, let $P'\in AB\;$ satisfy $BP'=AP.\;$ Then, since $BP=PQ,\;$ $PP'=PO,\;$ so that $\Delta POP'\;$ is equilateral, and $O\;$ lies on the perpendicular bisector of $PP'.\;$ By the construction, this is also the perpendicular bisector of $AB.\;$ Side $BC\;$ is treated similarly. It follows that $O\;$ is the circumcenter of $\Delta ABC,\;$ implying that $PQ\;$ is indeed its Euler's line.
Extra
The above confirms an old result that the Euler line in a triangle with an angle of $60^{\circ}\;$ cuts off an equilateral triangle. In such a triangle, the condition of the problem is both necessary and sufficient. This is because, by continuity, among all lines $PQ\;$ that cut off an equilateral $\Delta PBQ,\;$ only one may satisfy the condition $AP+CQ=PQ.$
Acknowledgment
The problem has been kindly posted at the CutTheKnotMath facebook page, along with his solution (Solution 1), by Leo Giugiuc. Leo credits the problem to Kadir Altintas (Turkey) and Ruben Dario (Peru).
- Condition to Have a 60 Degrees Angle
- Fermat in a Triangle with a 60 Degrees Angle
- Triangle with a 60 degrees angle
- Euler Line in a Triangle with a 60 Degrees Angle
- Euler Line Cuts Off Equilateral Triangle
- 9 Point Center on Angle Bisector
- Orthic Triangle in a Triangle with a 120 degrees angle
- Klamkin's Quickie via Peru Geometrico
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73581155
