Triangle with a 60 degrees angle

What Might This Be About?

Problem

In $\Delta ABC,$ $\angle BAC=60^{\circ}.$ $BE$ and $CF$ are two angle bisectors meeting at the incenter $I,$ $E\in AC,$ $F\in AB.$

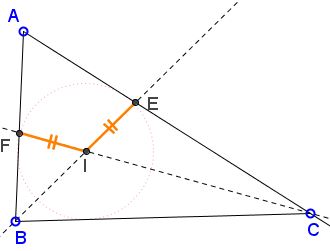
triangle with 60 degrees angle, problem

Prove that $EI=FI.$

Proof

$\angle ABC + \angle ACB=120^{\circ},$ implying $\angle EBC + \angle FCB=60^{\circ},$ so that $\angle EIF=\angle BIC=120^{\circ}$ and $\angle EAF + \angle EIF=180^{\circ},$ making quadrilateral $AEIF$ cyclic.

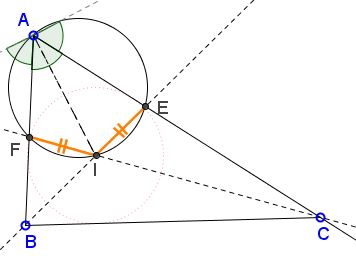
triangle with 60 degrees angle, solution

The chords $EI$ and $FI$ are equal as subtending equal inscribed angles.

Acknowledgment

The applet above illustrates a portion of Leo Giugiuc's result dealt with elsewhere.

Condition to Have a 60 Degrees Angle
Fermat in a Triangle with a 60 Degrees Angle
Triangle with a 60 degrees angle
Euler Line in a Triangle with a 60 Degrees Angle
Euler Line Cuts Off Equilateral Triangle
9 Point Center on Angle Bisector
Orthic Triangle in a Triangle with a 120 degrees angle
Klamkin's Quickie via Peru Geometrico

73361279