Klamkin's Quickie via Peru Geometrico
Source
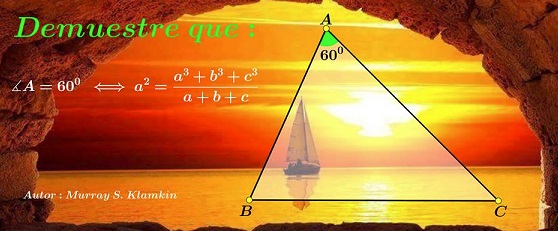
Solution
By the Law of Cosines, $a^2=b^2-bc+c^2\,$ iff $\angle A=60^{\circ}.\,$ That identity is equivalent to $a^2(b+c)=b^3+c^3,\,$ or $a^2(a+b+c)=a^3+b^3+c^3.$
Acknowledgment
I borrowed this problem from the Peru Geometrico facebook group. The problem is attributed to the late Murray S. Kamkin (probably one of his quickies.) There are several additional solutions available.
- Condition to Have a 60 Degrees Angle
- Fermat in a Triangle with a 60 Degrees Angle
- Triangle with a 60 degrees angle
- Euler Line in a Triangle with a 60 Degrees Angle
- Euler Line Cuts Off Equilateral Triangle
- 9 Point Center on Angle Bisector
- Orthic Triangle in a Triangle with a 120 degrees angle
- Klamkin's Quickie via Peru Geometrico
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73606321
