9 Point Center on Angle Bisector
What is this about?
A Mathematical Droodle
Created with GeoGebra, 22 November, 2016
Problem
The applet may suggest that
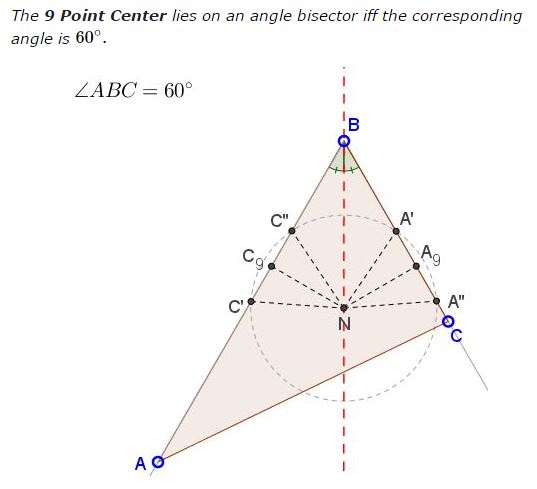
Solution
$\mathbf{If \;\angle B=60^{\circ}\; then\; N\in\ell_B}$
This is a consequence of the previous result: If $\angle ABC=60^{\circ}\;$ then the Euler line is perpendicular to the angle bisector: $OH\perp\ell_B.\;$ Since the circumcenter $O\;$ and the orthocenter $H\;$ are isogonal conjugate, $\Delta OBH\;$ is isosceles, and, therefore, its angle bisector from the apex is the median to the base. However, the midpoint of $HO\;$ is the 9 Point center $N,\;$ implying that $N\;$ lies on the angle bisector (of both $OBH\;$ and $ABC.$
$\mathbf{If\;N\in\ell_B\; then\; \angle B=60^{\circ}}$
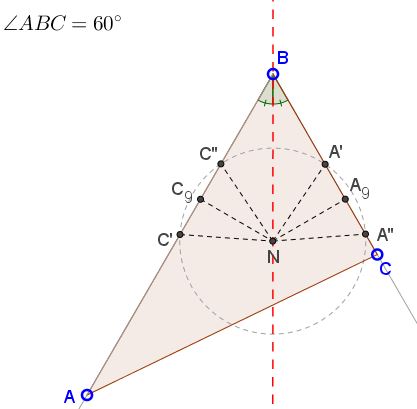
Define the midpoints $A',C'\;$ and the feet of the altitudes $A'',C''$ on $BC\;$ and $AB,\;$ respectively. Let $A_9\;$ and $C_9\;$ be the projections of $N\;$ on these sides. Then, since $N\in\ell_B,\;$ $NA_9=NC_9.\;$ Since the 9 Point circle passes passes through $A',C',A'',C'',\;$ $NA'=NC'=NA''=NC''.$
It follows that triangles $A_9NB\;$ and $C_9NB\;$ are equal, making the right triangles $C_9NC''\;$ and $A_9NA'\;$ also equal, such that $C''N=A'N\;$ and $\angle A_9NA''=\angle C_9NC''.\;$ From here, also, $\angle A'NB=\angle C''NB.\;$ Thus $\Delta BNA'=\Delta BNC''\;$ and, consequently, $BA'=BC''.$
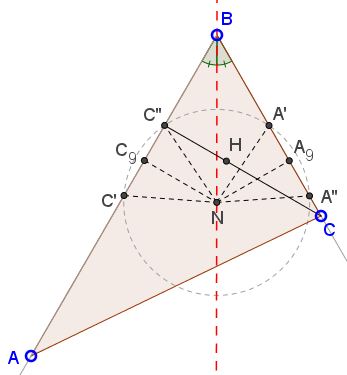
This means that in $\Delta CC''B,\;$ $2BC''=BC,\;$ hence $\angle CBC''=60^{\circ}.$
Acknowledgment
The statement above has been insipred by Ignacio Larrosa Cañestro's proof of a related result.
- Condition to Have a 60 Degrees Angle
- Fermat in a Triangle with a 60 Degrees Angle
- Triangle with a 60 degrees angle
- Euler Line in a Triangle with a 60 Degrees Angle
- Euler Line Cuts Off Equilateral Triangle
- 9 Point Center on Angle Bisector
- Orthic Triangle in a Triangle with a 120 degrees angle
- Klamkin's Quickie via Peru Geometrico
|Activities| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73609268
