The 80-80-20 Triangle Problem, Solution #5
| |
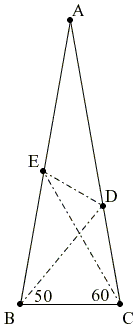
Let ABC be an isosceles triangle (AB = AC) with  BAC = 20°. Point D is on side AC such that CBD = 50°. Point E is on side AB such that BCE = 60°. Find the measure of CED.
|
Solution
Copyright © 1996-2008 Alexander Bogomolny
This is Solution 4 from [Knop].
Let F be on AB with BCF = 20°.
Then BFC = 80° = ABC, so that ΔBCF is isosceles and CF = BC.
Since also CD = BC and DCF = 60°, ΔCDF is equilateral and, in particular, DF = CF.
ΔCEF is isosceles because CEF = ECF = 40°. Therefore, DF = EF. It follows that F is equidistant from C, D, and E such that it serves the circumcenter of ΔCDE. CED is inscribed into a circle with center F and is subtended by the same arc as the central angle CFD. But the latter is 60°. Therefore, CED = 30°.
Reference
- C. Knop, Nine Solutions to One Problem, Kvant, 1993, no 6.
Copyright © 1996-2008 Alexander Bogomolny
|
