The 80-80-20 Triangle Problem, Solution #12

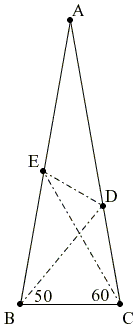
Let ABC be an isosceles triangle (AB = AC) with ∠BAC = 20°. Point D is on side AC such that ∠CBD = 50°. Point E is on side AB such that ∠BCE = 60°. Find the measure of ∠CED.

Solution

I picked this solution at the stackexchange forum. It is related to the solution #8, but approaches the configuration in a more symmetrical manner. The post at the stackexchange is under the moniker of Aryabhata. You'll notice that Aryabhata uses vertex names different from those at this site. I hope this won't cause any significant confusion.

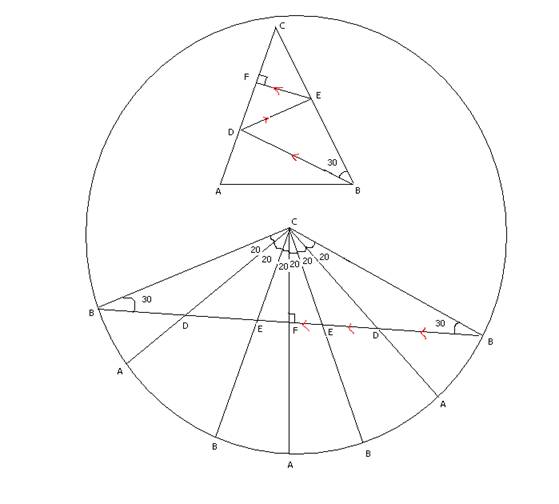
solution 12 to the classical 80-80-20 triangle problem

We can see that an 80-80-20 triangle is nothing but a part of the triangulation of an 18 sided regular polygon, whose 6 triangles are shown in the the bottom part of the circle above.

Now consider an 80-80-20 triangle (ABC on top part of figure) and shoot a light ray from one of the base vertices (B in the figure) at an angle of 50 degrees to the base (or 30 from one of the equal sides). (See the triangle in the top part of the circle and the red arrows)

We can show that the ray will reflect twice (first at D then E) and strike at a 90 degree angle the third time (F) i.e. after 5 refections, the light ray will return back to the vertex!

This reflection process can be pictured in another way, by reflecting the triangle each time instead of reflecting the ray (see the red arrows in the 6 triangles in the bottom part)

Now the point of the third reflection F (i.e. the 90 degree incidence point) is exactly the midpoint of the side on which the ray is incident on. This can be seen by considering the bottom part:

Consider the right most B and corresponding triangle CBF. This is a 90-60-30 triangle. Thus CF is half CB which is half CA.

(Back to triangle at top) i.e. F is midpoint of AC. Thus triangle ACE is isosceles, thus angle CAE = 20.

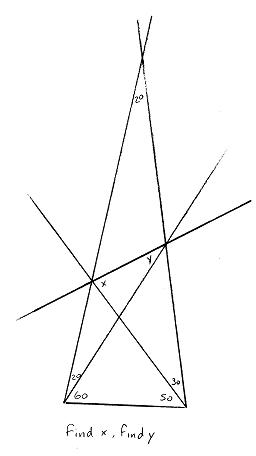
Thus, we see that angle BDE must be the angle x in the problem, which must be 180-(50+50) = 80. (as DE is BD reflected on AC). That angle y is 30, follows…

Note: To get more context about what x and y are, this was the figure when the problem was shown to me:

solution 12 to the classical 80-80-20 triangle problem, general problem

The 80-80-20 Triangle Problem

71544679