The 80-80-20 Triangle Problem, Solution #3

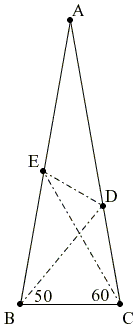
Let ABC be an isosceles triangle (AB = AC) with ∠BAC = 20°. Point D is on side AC such that ∠CBD = 50°. Point E is on side AB such that ∠BCE = 60°. Find the measure of ∠CED.

Solution

This is a trigonometric solution (Solution 2 from [Knop]).

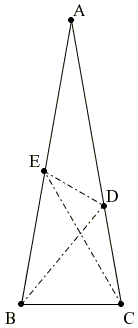
Denote the unknown angle CED as x. Then ∠CDE = 160° - x.

Apply the Law of Sines in ΔCDE:

CE : CD = sin (160° - x) : sin x.

And in ΔBCE,

CE : BC = sin 80° : sin 40° = 2cos 40°.

For, sin 2α = 2sin α · cos α.

Since ΔBCD is isosceles, CD = BC, which allows us to write a trigonometric equation:

sin (160° - x) : sin x = sin 80° : sin 40°.

This we are going to solve presently.

Using sin(180° - α) = sin(α),

sin (20° + x) = 2cos 40° · sin x = 2cos (60° - 20°) · sin x.

Using the addition formula for sine and the one for cosine,

sin 20° · cos x + cos 20° · sin x = cos 20° · sin x + √3sin 20° · sin x,

which simplifies to

sin 20° · cos x = √3sin 20° · sin x,

or,

ctg x = √3.

From which x = 30°.

Reference

C. Knop, Nine Solutions to One Problem, Kvant, 1993, no 6.

The 80-80-20 Triangle Problem

71534359