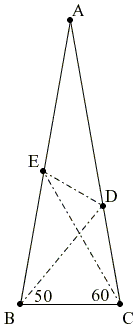
The 80-80-20 Triangle Problem, Solution #8   Let ABC be an isosceles triangle (AB = AC) with BAC = 20°. Point D is on side AC such that CBD = 50°. Point E is on side AB such that BCE = 60°. Find the measure of CED. Solution Copyright © 1996-2008 Alexander Bogomolny                           This is Solution 7 from [Knop] and is due to Alexander Kornienko, a high school student at the time. Reflect B in AC and C in AB to obtain B' and, respectively, C'. Now, AB'D = ABD = 30°. Further, B'AC' = 60° and AB' = AC' so it follows that B'D is the perpendicular bisector of AC'. Since AC'E = ACE = CAE = C'AE, we see that E is equidistant from A, C, and C'. E then lies on the perpendicular bisector of AC', i.e. on B'D. But then   CED = 180° - 40° - 40° - 70° = 30°. (This solution is neatly embedded into a configuration of an 18-gon.) Reference C. Knop, Nine Solutions to One Problem, Kvant, 1993, no 6. Copyright © 1996-2008 Alexander Bogomolny

28761648

Search:

All Products Apparel Baby Beauty Books DVD Electronics Home & Garden Gourmet Food Personal Care Jewelry & Watches Housewares Magazines Musical Instruments Music Computers Camera & Photo Software Sports & Outdoors Tools & Hardware Toys & Games VHS Computer Games Cell Phones

Keywords:

Latest on CTK Exchange Math Posted by Laura 2 messages 06:56 AM, Apr-15-08 Divisibility rules - Jargon buste ... Posted by Carolyn 2 messages 08:35 AM, Apr-04-08 drawing puzzle Posted by martin gran 31 messages 06:53 PM, May-09-08 conway's game of life Posted by frequency 0 messages 11:52 PM, May-12-08 Mistake on the page (an aside, Be ... Posted by Max 4 messages 10:28 AM, Feb-28-08 A Riddle Posted by idavis1 33 messages 06:59 AM, May-15-08 Josephus Flavius (correction) Posted by David Turner 1 messages 09:42 AM, May-14-08